Complex Dynamics and the Mandelbrot Set I

Possibly, potentially, the beginning of a series

There are myriad beautiful things in math—theorems, mostly—that the broader public has never heard of. One of the things that has entered the public consciousness, however, is the Mandelbrot set. Many, many people have been captured by the beauty of this pristine, mathematical object.

Created by Wolfgang Beyer with the program Ultra Fractal 3.

This object has become one of the standard examples of a fractal. Many people have invested absurd amounts of computing power into doing "zooms" on the Mandelbrot set—zooming in deeper and deeper on a specific point within it. (You can find some examples here and here links). This is about where people's knowledge stops.

I'm taking a class this semester where we will appreciate the beauty of the Mandelbrot set as mathematicians do: understanding it. As such, I don't know what in particular this series will hold! You'll be following along with me as I learn.

With that in mind, I must ask you to keep in mind that this is more akin to notes from a classmate. I am not an expert in these things, and it is more than possible I'm wrong about something. I'm also going to try and write in such a way where, though I include the technical details for those who want them, it is nonetheless readable for those who don't. Many of the footnotes will hold more technical details. If I say something confusing, ask questions in the comments—I really don't mind.

---

An easy example

Roughly speaking, the Mandelbrot set is a chart of what happens when you iterate a certain function on the complex plane.¹ To explain what I mean, let's look at some simpler examples.

Consider the function f : ℝ → ℝ defined by

\(f(x) = x + 1.\)

If you haven’t seen it before, ℝ just denotes the real numbers—the number line. We're going to consider what happens as we repeatedly apply f to the number line. That is, we're going to look at the points

\(f(x), f(f(x)), f(f(f(x))), ...\)

and see what happens for various values of x.

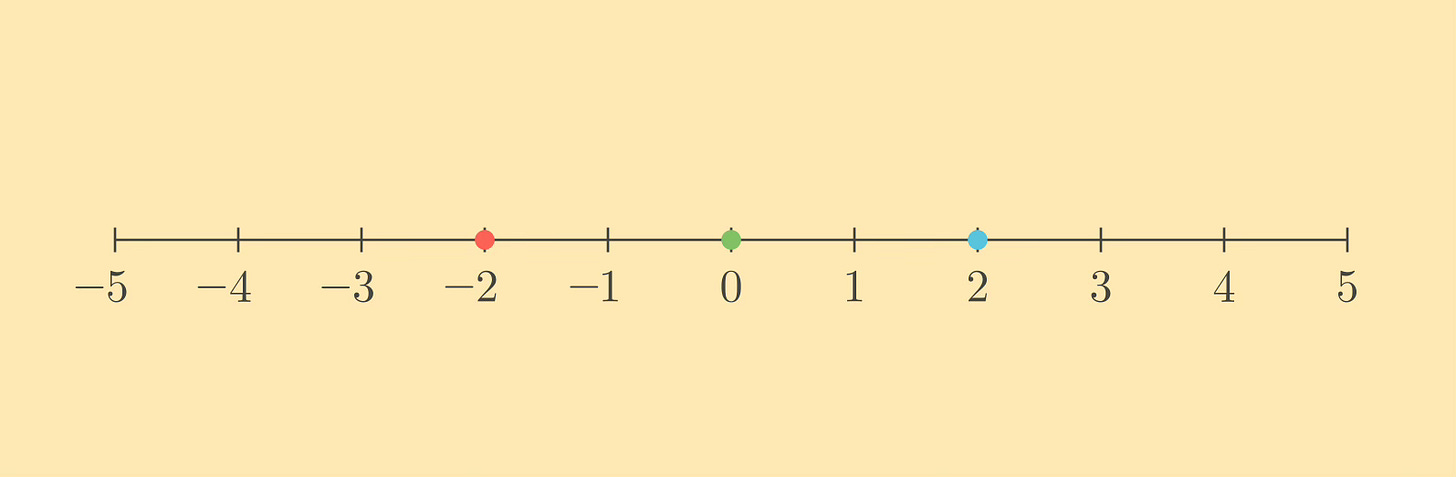
Here's our starting real number line. I've put a red dot at negative two, a green dot at zero, and a blue dot at two. The first time we apply f, what happens? Well, everything shifts forward by one:

Now our dots are at negative one, one, and three. Of course, if we apply f again, they move forward by one again:

What this picture is telling us is that f(f(−2)) = 0, f(f(0)) = 2, and f(f(2)) = 4. Rather than using a ton of f's and parentheses, mathematicians use shorthand:

\(f^2(x) = f(f(x))\)

And of course we aren't restricted to using two in the superscript, we can use three, four, etc. Since our function is so simple, we can give a closed expression for any iterate fⁿ(x), namely,

\(f^n(x) = x + n.\)

Simple enough, right? Applying "add one" n times is of course the same as adding n, once.

Because this function is so simple, there's not very much interesting behavior. One question we can ask, though, is whether or not the sequence f, f², f³, ... converges to anything. That is, is there some function that the sequence of iterates of f gets closer and closer to?²

At first, it might seem like no. It's not as though there's any sort of shrinking or expanding behavior—the points don't all get closer and closer to zero, for instance. But this sequence does converge to something.

Pick any number x ∈ ℝ. It can be positive, negative, zero, anything. Now, pick some super large positive integer M. Is there an iterate fⁿ(x) such that fⁿ(x) > M? Indeed there is. All we need to do is pick n such that

\(x + n > M   ⟹   n > M − x.\)

As long as n > M − x, fⁿ(x) will surpass M. Since M and x are arbitrary, this means that every number is eventually larger than M, for any M. In this sense, we can say that the sequence f, f², ... converges to...∞! In particular, we say that this sequence of functions {fⁿ(x)} converges to the constant function

\(g(x) ≡ ∞.\)

The triple−bar equals sign here just means that g is identical to, or everywhere equal to, ∞. While unintuitive, really what this is telling you is that every single point on the number line eventually passes any finite number.

---

Another example

Let's consider a slightly more complicated example. Let f : ℝ → ℝ be defined by

\(f(x) = x/2.\)

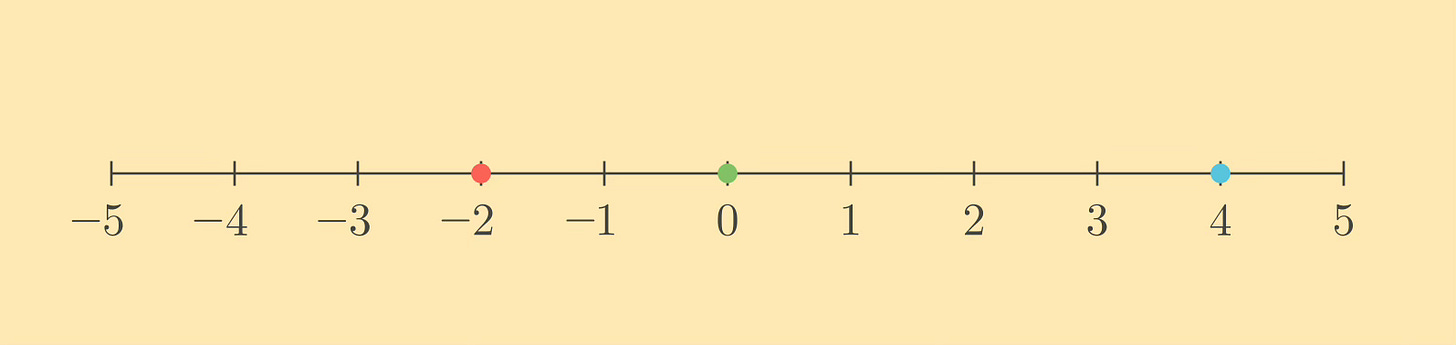
What happens under iterates of this map? I'll once again put some dots on the number line: this time red at negative two, green at zero, and blue at four:

Since we're dividing by two, the first application does this:

Something interesting has already happened here—zero hasn't moved. Since the iterates of f consist in dividing by two multiple times, and dividing by two once didn't move zero, neither will any other iterate of f. This means that zero is a fixed point of f.

Clearly, if we keep applying f, the red and blue points will keep moving towards the green point. Since our function is relatively simple, we can again find a nice closed form for fⁿ(x), namely

\(f^n(x) = x/2^n.\)

Since everything gets closer and closer to zero, a natural guess would be that this converges to the constant function g(x) ≡ 0. Indeed, this is what happens. If we choose some arbitrary small |ε|, we can always make fⁿ(x) smaller than |ε| with the right choice of n:

\(x/2^n < |\varepsilon| \quad \Longrightarrow \quad n > \log_2(x/|\varepsilon|).\)

Once again we have a series of functions that, while none of them is individually the zero function, the series nonetheless "approaches" the zero function. This function is more interesting than our first function, however—we have this special point, x = 0, where the function is fixed.

---

So what is the Mandelbrot Set?

The first two examples that we've seen are examples of what are formally called discrete−time dynamical systems:

Definition: A discrete−time dynamical system is a function f : X → X for some space X, where we consider iterating—repeatedly applying—the function f on X. (Think of this as applying the function f to the space once every second, or something similar).

For what we're doing, we will most often consider X = ℂ, the complex numbers,³ or X = ℂ̅, the complex numbers together with a single "point at infinity", denoted by ∞. Often, ℂ̅ is called the Riemann Sphere, because you can think of taking the plane of complex numbers, curving it into a sphere, and then adding the north pole, ∞, which would otherwise be missing.

From Apostol’s 1973 book on analysis.

Note that on the Riemann sphere, it doesn't matter which direct you go—if your number gets really large, positive or negative, it will "tend toward" infinity.

We can almost define the Mandelbrot set, but we need to see one more example. Let f : ℂ̅ → ℂ̅ be defined by f(x) = x². What does this function do?

Because we're working in the Riemann Sphere, there's a lot more interesting behavior that we can get than if we were just working in the real numbers. There's a few different kinds of behavior that we'll check for:

• Fixed points are points z₀ where f(z₀) = z₀. The name is apt; they're fixed under f.

• Periodic points are similar to fixed points, but we only require that fⁿ(z₀) = z₀ for some n. These points will have some sort of "cycle" that they follow.

• Eventually periodic points are similar to periodic points, except it may not be that the original point is part of the cycle; for these, we have fⁿ(z₀) = fᵐ(z₀) for some n, m.

And of course, we'll also check for points that tend towards other points—like we saw with everything tending towards zero in our f(x) = x/2 example.

So what happens with f(z) = z²? Well, for starters we can see straightaway that 0, 1, and ∞ are all fixed points of f. That is,

\(f(0) = 0,   f(1) =1,   f(∞) = ∞.\)

Further, 0 and ∞ are attracting fixed points. This means that, around 0 and ∞, the points near them tend to converge to them under f. Take a number like z = 1/2; if you keep squaring it, you get 1/4, then 1/8, and so on—it goes to zero. As long as |z| < 1, in fact, it will tend to zero. This region is called the attracting basin for zero.

Similarly, for ∞ if we take numbers |z| > 1, then as we square them they will get bigger and bigger and approach ∞. Thus, |z| > 1 is the attracting basin for ∞.

Perhaps this is easier to see if we write our numbers in polar coordinates. Usually, complex numbers are written with the form

\(z = a + bi\)

for a, b ∈ ℝ. But we can also write them in a different way, based on magnitude and angle:

\(z = re^{i \theta}.\)

Here, r is our magnitude (really, it's the length of the radius) and θ is an angle from 0 to 2π.⁴ Since r is a magnitude, it's just some real number, and we know how squaring real numbers work. If r > 1, then fⁿ(r) → ∞; if r < 1, then fⁿ(r) → 0. This is exactly equivalent to the cases |z| > 1 and |z| < 1, respectively.

So we understand now what happens when |z| > 1 and when |z| < 1; what about when |z| =1?⁵ This is a much harder question. We might guess that, since 1 is a fixed point, points on the unit circle will eventually converge to 1. Unfortunately, this couldn't be further from the truth.

For starters, let's check out the value

\(z = e^{2\pi i /3}\)

What happens as I square this? Well, for any e^{iθ} (remember that this is essentially a rotation by θ), we have

\((e^{i \theta})^2 = e^{i \theta} e^{i \theta} = e^{i 2 \theta}.\)

In other words, squaring doubles the angle. So for our value z = e^{2πi/3}, we get

\(f(z) = z^2 = e^{4\pi i / 3}.\)

What happens when we do this again? Well, the angle doubles again, so we get

\(f^2(z) = f(f(z)) = f(e^{4\pi i /3}) = e^{8\pi i / 3}.\)

But we can't stop here, because 2π radians is a full rotation, which means

\(e^{2\pi i} = 1.\)

So really, we get

\(f^2(z) = e^{8\pi i /3} = e^{6\pi i /3}e^{2\pi i / 3}= e^{2\pi i / 3}.\)

So...we're right back where we started. This means that z = e^{2πi/3} and z² are periodic points with period 2.

What about

\(z = e^{2\pi i / 7}?\)

Well, quick calculation shows that

\(f(z) = e^{4\pi i / 7}, \; f^2(z) = e^{8\pi i / 7}, \; f^3(z) = e^{16\pi i / 7} = e^{2\pi i / 7}.\)

So this means z, z², z⁴ are all periodic points of period 3.

Similar work shows that indeed, you can find periodic orbits in |z| = 1 of any length whatsoever. That is, for all positive integers n, there is a point in |z| = 1 such that z has period n.

But it gets worse. If you choose certain irrational values of θ, then it won't be periodic at all! Rather, it will keep bouncing around the unit circle, never to reach the same place twice, chaotically traveling without ever finding a pattern. Because of this, the point z = e^{iθ} will have an orbit that is dense in the unit circle. Roughly this means that, if you pick any random point x on the unit circle, at some point fⁿ(z) will be as close as you like to x.

This region where the map z ⟼ z² is chaotic is called the Julia set of f. Its complement, the region where points behave nicely—they converge—is called the Fatou set of f. We often denote the Julia set of a function by J(f). We'll define these more formally next time. As we’ve seen, for the map z ⟼ z², the Julia set is the unit circle.

With this final example we can now define the Mandelbrot set. The Mandelbrot set M is the set of all c ∈ ℂ such that the function

\(f_c(z) = z^2 + c\)

does not go to infinity at z = 0. In other words, a point c is in the Mandelbrot set M if and only if the set

\(\{f^n_c(0) \mid n \in \mathbb{N}\}\)

does not go off to infinity.

The first published picture of the Mandelbrot set—from 1978.

---

Normally, I would have some summary here of what we've covered today, and talk about what's coming next. But, because of the nature of this work, I don't know what's coming next. About all I can say is that things are likely to get more technical and involved from here on out, so buckle in! I'll do my best to explain things intuitively before giving formal definitions, but this may not always be possible. Some problems you might stop and think about:

1. Can you find an explicit expression for points with period n under the map z ⟼ z², for arbitrary n?

2. What would you expect the Julia set to look like for f_c, if c is some value close to zero?

1. Technically, this is a lie—it’s more like a family of functions, but we’ll get there in due time.

2. In particular, the kind of convergence we want is uniform convergence on compact subsets. If you already know what this is, great; if not, we’ll go into it more next time.

3. If you aren’t super familiar with complex numbers, I highly recommend this series by Welch Labs on YouTube:

4. If you haven’t seen this before, e^{iθ} is equivalent to rotation by θ. We generally think of angles as radians, where 2pi is equivalent to 360 degrees.

5. If you took trigonometry in high school, you might remember the unit circle—secretly, the unit circle is the set |z| = 1 in the complex plane.