Introduction to Group Theory I
What even is a group, anyway?
If someone says the word "Algebra" to you, what do you think of? If you're like most people, probably something like: Find the solutions to the equation
While this is indeed a section of what modern-day mathematicians would call "Algebra", it is a rather small part of it. A lot of Algebra is nowadays concerned with structure. What are the important laws for a set to obey for us to be able to do "algebra" on it? When can you ask questions like "solve this quadratic?" These are the kinds of questions you will find nowadays in an undergraduate or graduate (abstract) algebra course. Amongst other things, such a class is where mathematicians define Groups, Rings, and Fields. All three of these notions will come up over the course of this project.
As you may suspect from the title, we're going to start with Groups. Groups are perhaps the simplest kind of algebraic structure that is truly important and useful. They are important for us, additionally, because a lot of the later tools we need will be expressed in terms of groups. Before we get to the formal definition, I want to show you an example.
Example 1: A Clock Face
Imagine, if you will, a standard 12-hour clock face. (For some of my younger readers, this may prove to be quite the challenge.)

If we ignore any idea about minutes and seconds, and just consider the hour hand, we can see some important facts about the clock. First, we all know that adding twelve hours to the clock will not move the hour hand. That is, on a clock, if x is any number of hours,
Mathematicians have a special name for a number that acts like this - we call it the identity. So, on the clock face, 12 is our identity. Next, we know that addition satisfies the associative property. I think this is best explained by example. If I start at 3, go 4 hours forward, and then go 5 hours forward, I get to 12. If I instead add the 4 hours and the 5 hours first, I get 9 hours - and if I go 9 hours forward from 3, I also get to 12. In mathematical notation, this would be expressed as:
Of course, here, the specifics of the numbers don't matter, so we can write this using variables instead:
This is precisely what is meant by the associative property. In normal english, if you're adding three things, choosing which two to add first does not change the outcome. Similar to this, our clock face is commutative:
As an example, we all know that 3 + 7 is the same as 7 + 3.
The last property is a little more subtle. Choose any number on the clock face, let's say 4. If we add 8 to 4, we get 12, which is our identity. (Note that 4 is the inverse of 8, too.) We can do this for any number, of course, not just 4. Mathematicians call 8 the inverse of 4, and the existence of inverses is our final ingredient.
The Definition
Now that we've seen all these words, we can finally define a group. Don't worry; once I give the statement, I'll unpack any other words we haven't defined yet.
A group is a pair (G, •), where G is a set whose members we call elements, and • is a closed binary operation on G. The dot is used as a stand-in: it could be addition, multiplication, or some other operations we'll see later. Further:
The binary operation • is associative on G: that is, for all a, b, c in G, we have
There exists a unique identity element e in G, which satisfies, for all a in G,
\(a \cdot e = e \cdot a = a.\)For every a in G, there exists a unique b in G, commonly denoted a^-1 and called the inverse of a, which satisfies
\(a \cdot b = b \cdot a = e. \)
That's the definition of a group! Hopefully, most of those words don't scare you. And just in case, if you don't know what closed means, that just means that if I take x and y in G, and I apply the operation x • y, then that will also be in G. We wouldn't want to be thinking about the clock face, but then say 4 + 9 = 13, since 13 is not on our clock. Instead, on our clock we would say 4 + 9 = 1.
As we saw with our clock face example, some groups are also commutative. If your group is commutative, then it always satisfies the following property:
Notice that commutativity is not a requirement for something to be a group. In fact, our next example will not be a commutative group - the order will matter. Important side-note: often, commutative groups are also called Abelian groups.
Example 2: The symmetries of a triangle
Now that we've defined what a group is, we can look at another example which has a slightly less intuitive structure: the symmetries of a triangle. Consider, if you will, an equilateral (equal-sided) triangle. For reasons that will become apparent, I'm going to label the vertices 1, 2, and 3:
What we're going to consider here is all of the possible "moves" that we could do to the triangle that would leave it in the "same place". What I mean is, if I removed the labels, what moves could we do where, at the end, the triangle would look the same? Well, for starters, we could...do nothing. That counts as a "move" in math-land, and this is actually a very important move - it's our identity element, e. We could also rotate it 1/3rd of a full rotation:
We're going to need a way of representing this element, so let’s call it r. Seeing that we can rotate 1/3 of a full rotation, we can just as easily rotate 2/3rds:
You might think that we need another new symbol for this 2/3rds rotation, but actually, this rotation is the same as rotating by r, and rotating by r again. This action of "do something, then do something again" is exactly our binary operation here: mathematicians call it composition. We're also going to write
just for convenience. Mathematicians are lazy.
One important thing to note is that, in this case, we are going to read the order of the elements from right to left. That is, if I write
the way we’re going to read this is applying b first, and then a. I realize this is a strange thing to do, but I promise you there is a good reason for this, which we’ll get to in the next installment.
We could try adding a third rotation, but this would get us back to where we started. This is an important fact, though, because it tells us that
This is an important fact, or relation, for us to keep in mind. Now, you might be wondering, "what else is there?" Great question! I'm glad you asked. There's one other important kind of move we can do to our triangle: reflection.
Notice that when we rotate the square, all three of the numbers move. When we reflect, however, we choose a number to leave “fixed” (in this case, 1) and the other two swap places. None of our elements so far give us this move, so we do indeed need a new symbol for it: we'll call it s. There are two other reflections, but as before, we eventually see that the other two reflections are just s, combined with a rotation:
Importantly, we should check to see if our group is commutative. One quickly runs across the fact that r • s ≠ s • r:
This means our group is not commutative, since the commutative law (a • b = b • a) does not always hold.
So far, we've discovered six symmetries of a triangle:
And, try as you might, you won't be able to find another symmetry that can't be written as a composition of r's and s's. We have found all the possible symmetries of the triangle. Lets check and see if this is a group:
We'll call our set of elements D_6 - I'll explain why in a minute - and of course our binary operation • is composition. Clearly, any two symmetries composed with each other will give us another symmetry, so • is closed on D_6.1
Associativity can be checked by hand, but luckily we don't have to do that. It's well-known that composition of this kind is associative.
We do indeed have our identity element e.
Finally, I will leave it as an exercise to the reader to show that every element in D_6 has an inverse.
Summary
We've covered a lot of ground in this article. Give yourself a pat on the back! I'm still hammering out the format of these things, but I think at least for the first few articles I'm going to give quick summaries of all the important details.
Modern-day algebra is very concerned with structure. The simplest structure that's extremely important is called a Group.
Groups are a set of elements and a binary operation, such that the operation is associative, the group has a unique identity, and every element has a unique inverse.
We also saw two important examples: the clock face, which we will give a name in the next article or two, and the symmetries of the triangle, D_6.
Unfortunately, it is here I must break the news. I am going to state exercises at the end of each article.
Don't run! They're optional.
That being said, I am firmly of the belief that there is no substitute for doing math. If you really want to understand the things you're reading about, you have to work through a couple problems. They are optional, and I will supply solutions at the end of the next article, but I would highly recommend trying them if you feel so inclined. I will make it abundantly clear if I have stated a problem I believe to be difficult, too - most problems should be reachable, if you understand the article.
Exercises
1. For each element of D_6, find an inverse for that element. (Don't worry about the uniqueness of the inverse - we'll show that in full generality next time.)
2. Show that the symmetries of a square, which is called D_8, is a group. You can assume that composition is associative.
There is no one standard convention for the notation of the dihedral groups. Some people, as I have done here, call the group of symmetries of the regular n-gon (that is, n-sided polygon) D_{2n}, since there will be 2n elements in that group. Other people prefer D_n, since it is the symmetries of the n-gon. Both are fine, but one must choose a convention.


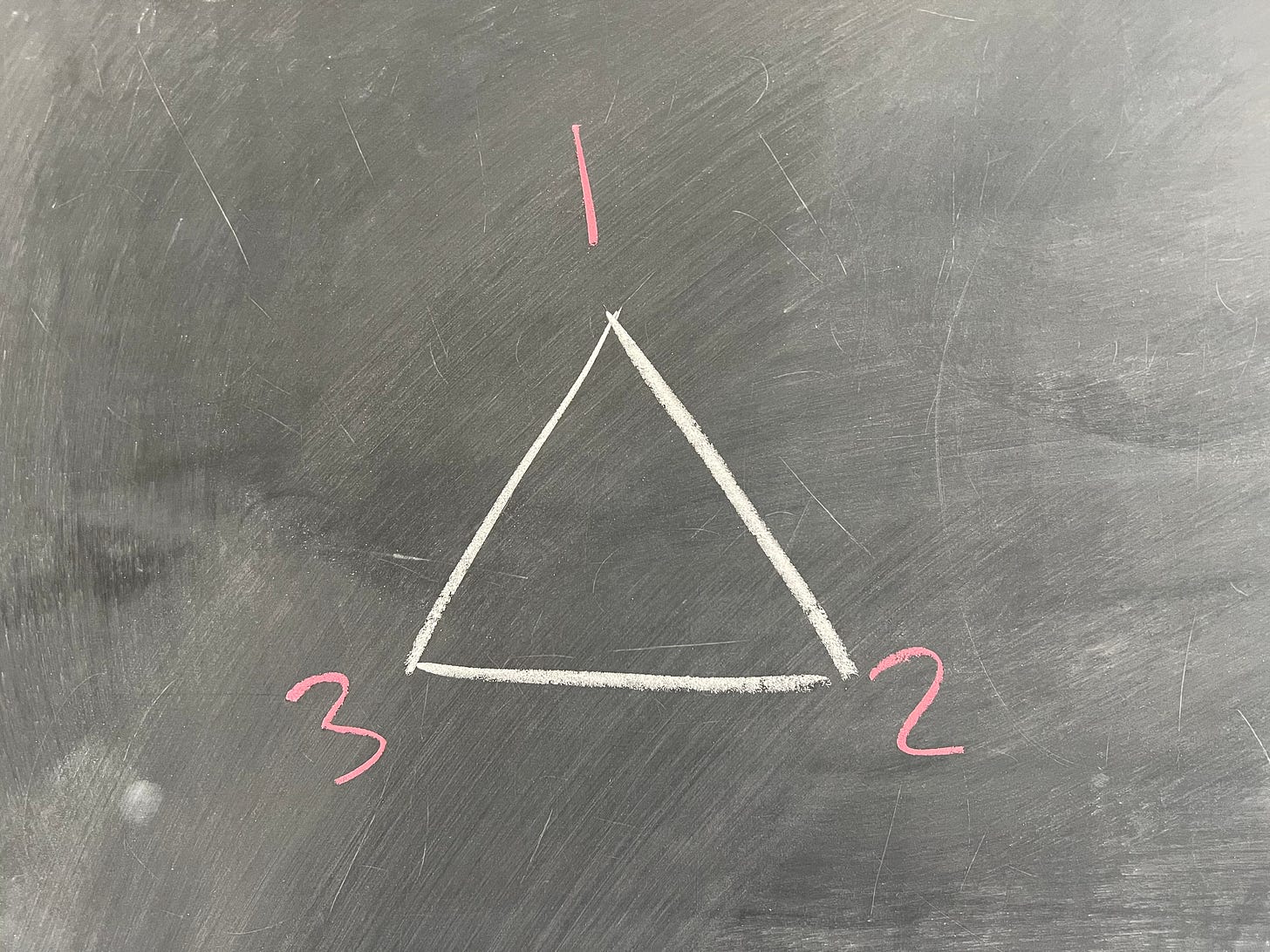
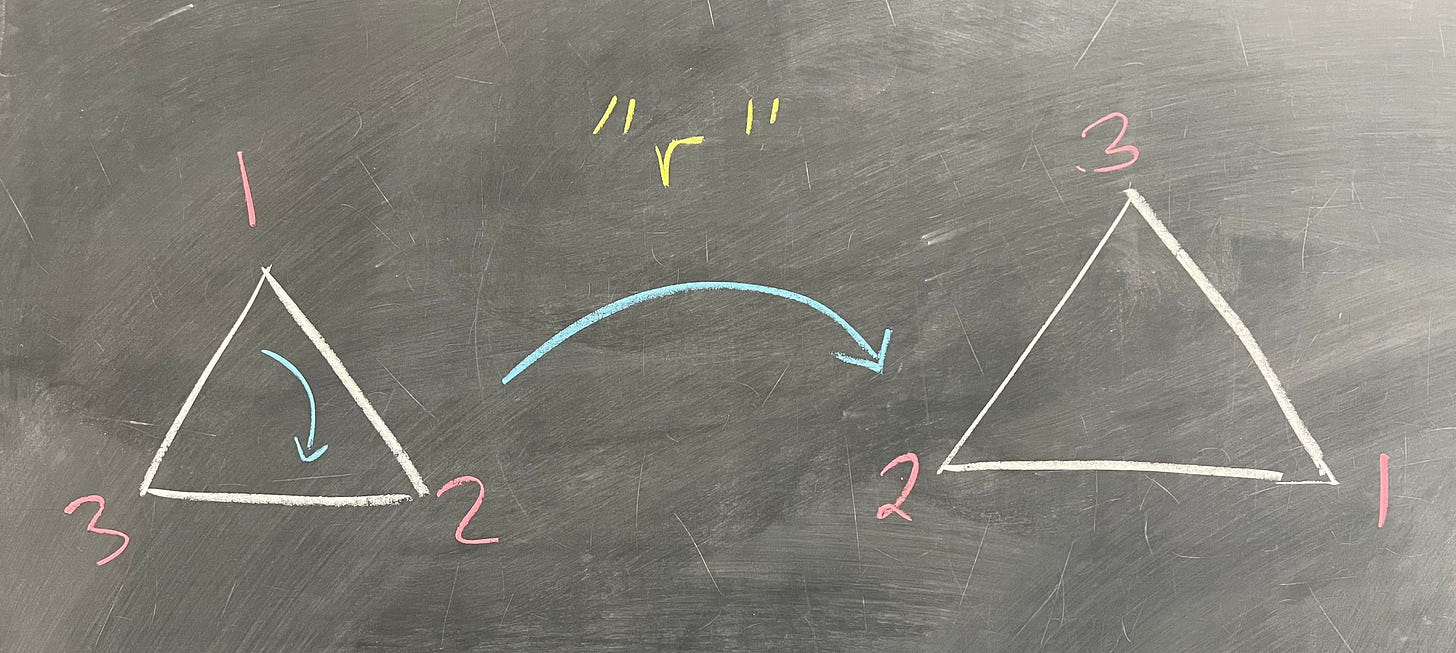


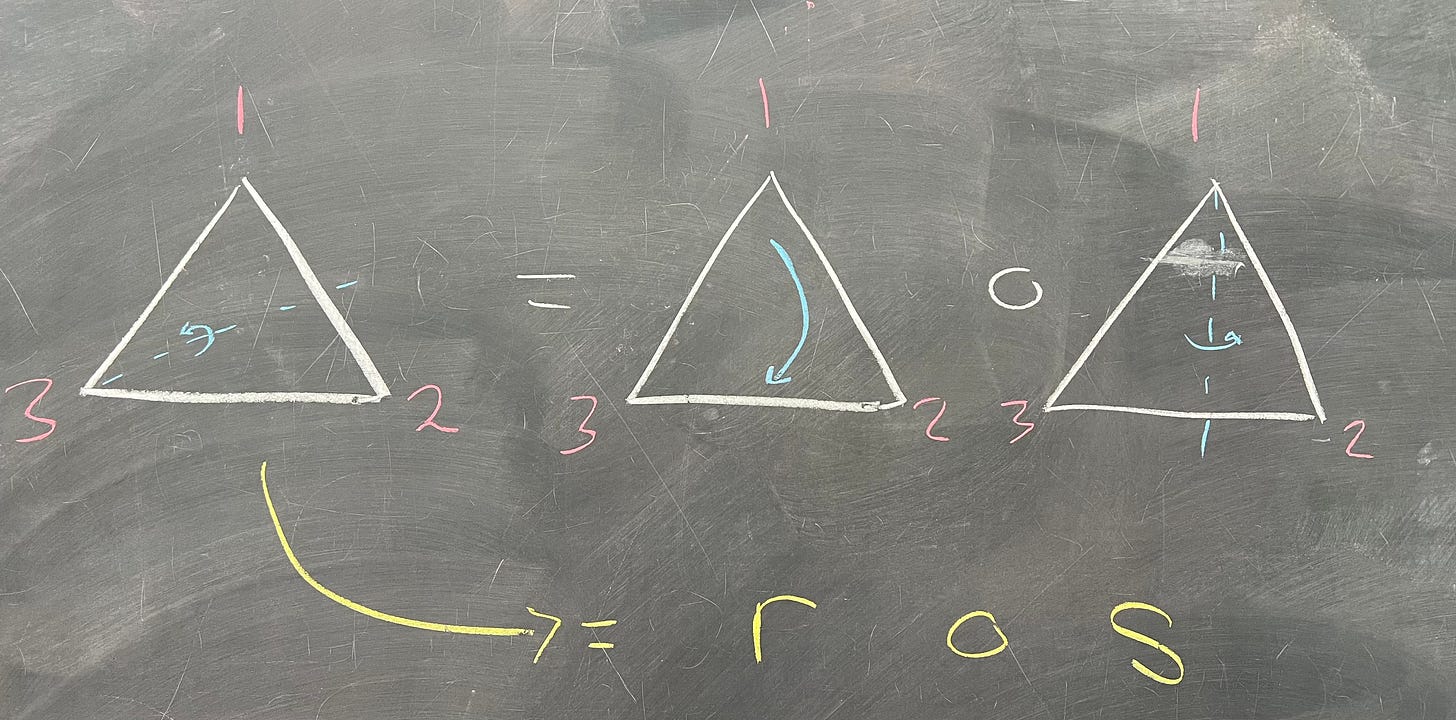
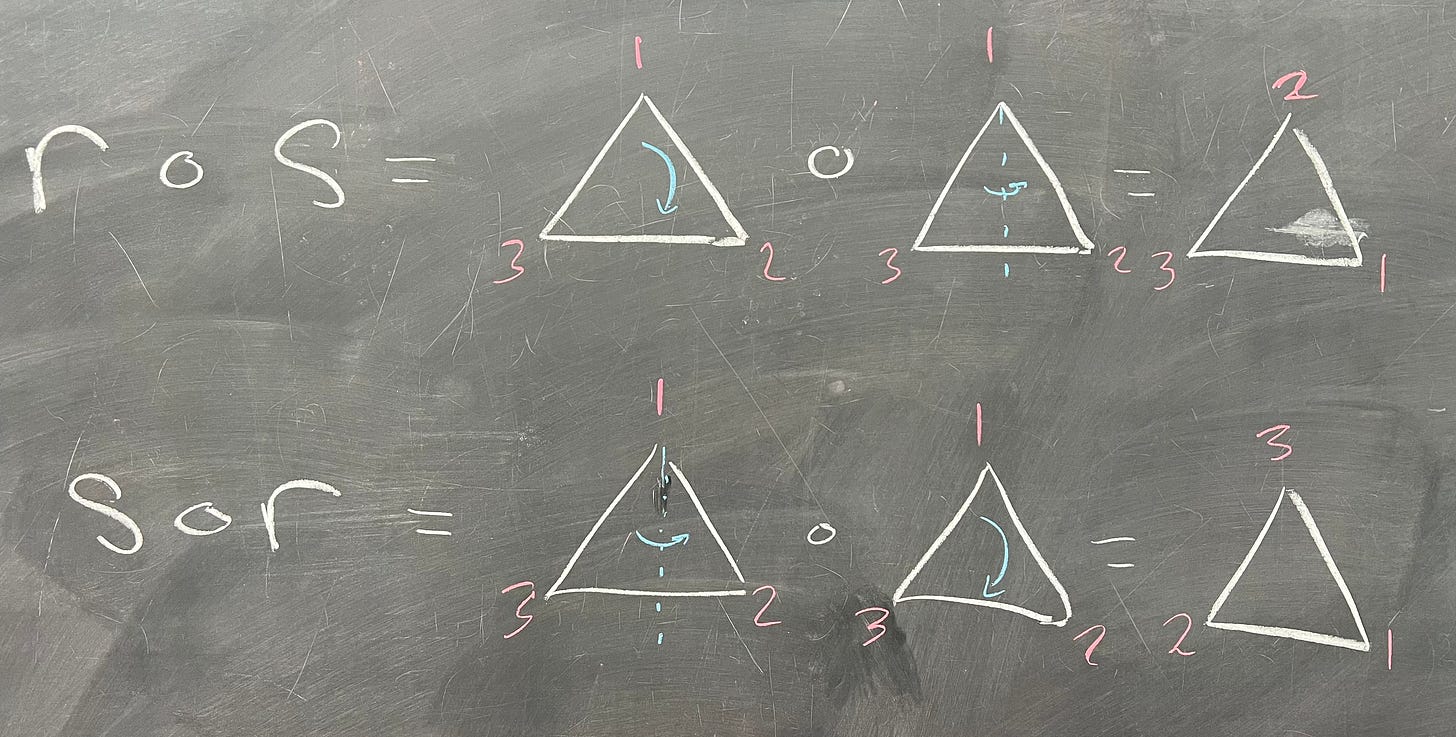
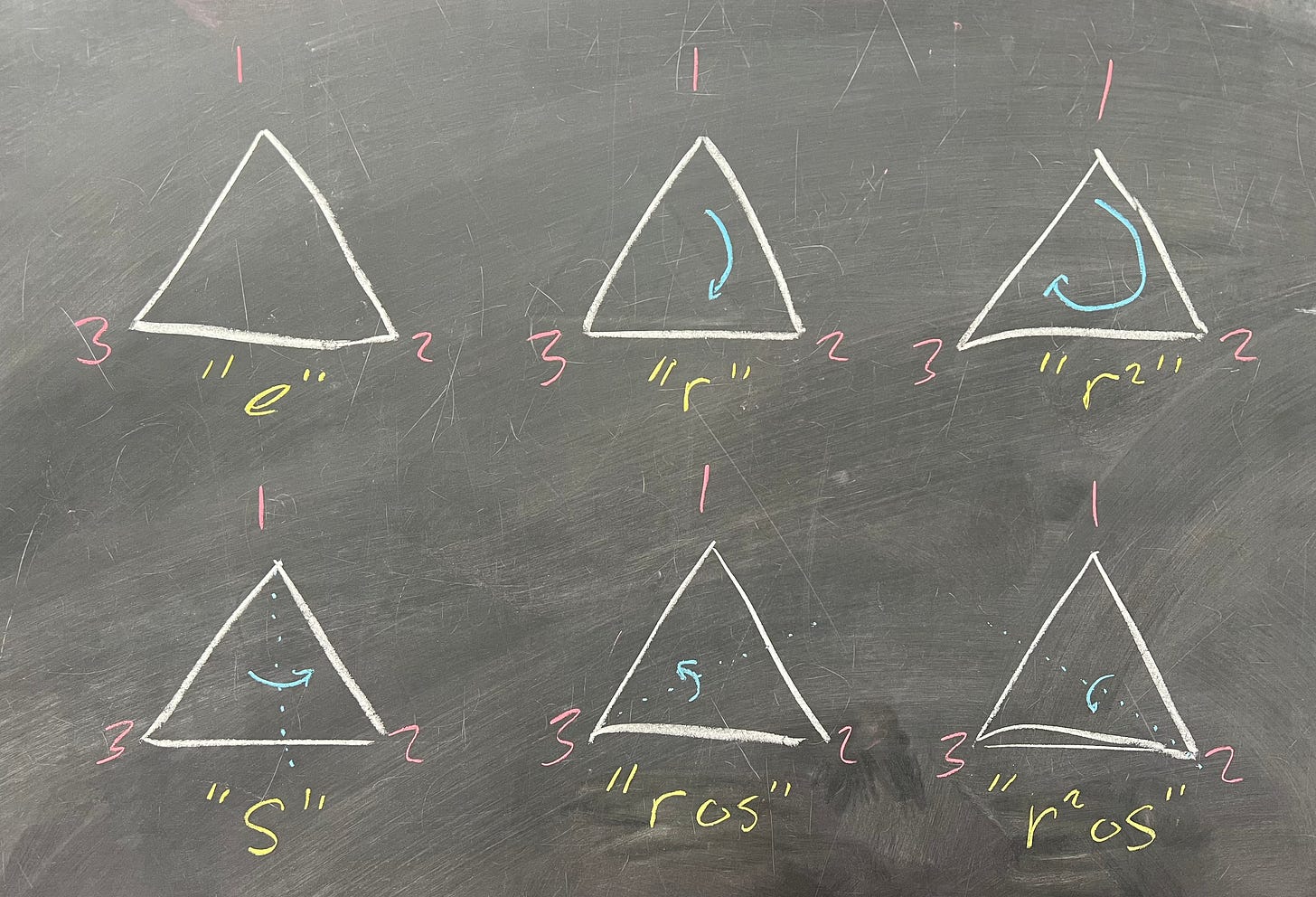
Math… a topic in which I lack quite dearly as a philosophizer. I appreciate your encouraging explanations! Informative and resourceful :)
You do great work explaining math topics. I read it like a newspaper in the morning. Thank you for doing this. I appreciate your work!