Introduction to Group Theory III
Wait, there are groups inside of groups?
A natural question, when learning about groups, is "can big groups contain smaller groups?" We'll spend today answering that question, but more importantly talk about the ways in which we can find the answer to that question.
Last time, we saw one of our long-term companions on this walk - the permutation group. More specifically, we talked about the group S_3 in some detail, and discussed at a ten-thousand-foot level the permutation groups S_4, S_5, S_n, etc. S_3 will be our main character for the next week or two - we're going to use this group to get some examples of very important ideas in group theory. We'll also return to our clock-face example, and finally give it a proper name.
Subgroups of groups
The answer to our question, unsurprisingly, turns out to be yes, and mathematicians call these subgroups.
Formally, a subgroup of a group (G, •) is a set H⊆G (this ⊆ symbol just means H is contained in G - think of it like ≤ but for sets), that is closed under • and is itself a group. Since H can be the whole set, G is a subgroup of itself. We call G an improper subgroup of itself - all other subgroups are proper. Likewise, the group {e} that contains only the identity element is called the trivial group, and is considered to be a trivial subgroup of G. All other subgroups are called non-trivial. We write
to mean that H is a possibly improper subgroup of G, and
to mean that H is a proper subgroup of G. This should make sense - if H is a proper subgroup, then there are less things in H than in G. If H might be improper, then H could have just as many things as G.
As usual, it's very helpful to have an example or two of this abstract definition - examples are easier to remember than definitions. So let's take up our main character of the day, S_3. Does S_3 have any subgroups? Well, according to our definition, yes: there's the trivial subgroup, which is just the "do-nothing" permutation, the identity, and there's the improper subgroup, which is just S_3 itself. As great and important as these groups are, as subgroups they're kind of...boring. They don't really tell us anything new. Let’s try to find some non-trivial, proper subgroups of S_3.
Subgroups of S_3
Beyond the identity element, there are two different kinds of elements in S_3: swaps, and cycles. I'm calling the elements (1 2), (1 3), and (2 3) "swaps" because they each do the same kind of thing - they swap two elements, leaving the third one fixed. The last two elements, (1 2 3) and (1 3 2) are "cycles" because they cycle around all our possibilities. Every number has to move, if we apply a cycle. Since we're talking about subgroups, lets try and build a set H such that H is a subgroup of S_3.
Well, first, if H is to be a subgroup, it has to have the identity, so we're always going to put e into H. We want a non-trivial group, though, so we need to pick another element of S_3. Let's take (1 2 3). Is
closed under our operation? Actually, no, it isn't. (1 2 3) • (1 2 3) is not (1 2 3) or the identity, but something else.
One thing we didn't touch on last time is how to compute the composition of permutations. This can be tricky for people, so I'm going to slow down and try to explain this carefully; I am also asking for your grace, as the reader, if I fail to explain this well.
Where people most often get tripped up is they think the permutations are telling you where the objects 1, 2, 3, etc., go. This is actually not true! What permutations tell you is where the object in place one goes, where the object in place two goes, etc. For example, our permutation (1 2) is telling you that whatever is in place one goes to place two, and place two to place one.
The permutation is not about the objects that move, but the arrows. So with that in mind, let's think about how we would calculate something like (1 2 3) • (1 2 3). Sidenote: often mathematicians drop the • and just write it as you would multiplication, even when the binary operation is not multiplication. That is, we often write
Mathematicians are lazy. For clarity, I will do my best to remember to use the dot, but I'm sure I will forget.
So with this in mind, how do we compute (1 2 3) • (1 2 3)? Well, one way is to think about this place by place. Let's start with the first place. We're going to imagine what happens to the object in place 1 as we apply these permutations, and we're going to write that like this:
Importantly, we think of the permutation closest to (1) as going first. Permutations get applied right to left. Now that we've got all this notation out of the way, we can finally start calculating. In the permutation (1 2 3), the first place gets sent to the second place:
Now we apply (1 2 3) again, to find
What this tells us is that ((1 2 3)•(1 2 3))(1) = (1 3 ...). We know that the object in the first place, after applying (1 2 3) twice, gets sent to the third place. Where does the third place go? I'll leave it to the reader to check the calculation should they so desire - this is a good way to make sure you're following the concepts - but what we get is
So, if we want our set to be closed, which we need for it to be a subgroup, we need to also include (1 3 2). That is, our set H is now
We have to check and make sure that this is now a closed set. First, note that
(1 2 3)•(1 2 3)•(1 2 3) is the identity, since 1 -> 2 -> 3 -> 1, and similarly for 2 and 3. In other words,
From this, we can actually conclude that our set H is closed! This is because every element in H that is not the identity is a power of (1 2 3), and having three copies of (1 2 3) gets you back to the identity. So, any possible element we can make, from only things in H, will have the form
And, if n is bigger than 3, we know that every multiple of three in n just gets us back to the identity. That is, (1 2 3)^6, (1 2 3)^9, etc, are all the identity, which means, for example,
The binary operation •, which is in this case composition, is clearly still associative since it is associative in all of S_3. We have the identity, and I leave it to the reader to double check that each element in H has an inverse (really, we have already checked this if you think carefully.) Great! That means H is a subgroup of S_3. This subgroup has a name - it is called C_3, the cyclic group of three elements. We'll talk more about cyclic groups later, but essentially, a cyclic group is a group that can be generated by one element. In this case, our generator is (1 2 3). Another way of saying this is that, if G is a cyclic group, then there exists some g in G such that every element can be written in the form
for some power n.1
You might have noticed that, just by nature of choosing (1 2 3), we also had to include (1 3 2) in H, so we don't need to see what happens if we start with H just containing e and (1 3 2) - we'll get the same subgroup. What happens if we start with
Consider the element
We see that 1 goes to 2, and then 2 goes to 1. Similarly, 2 -> 1 -> 2. So, H is already closed! Of course, (1 2) is not the only swap in S_3 - there is also (1 3) and (2 3). Let's call those sets J and K. That is, we have
There's something weird going on with these three sets. If I relabeled each of the swaps and called them all g, then they would look exactly the same. Moreover, they would behave exactly the same. Something fishy is going on here...
Subgroups of the clock face
We're going to do one more example. Let's go back to our clock face. There is a name for this group: it is called
where for some reason, standard notation is to use "Z" for "Zahlen", which is German for "integer". The integers are called ℤ. This is a special font, called "Blackboard Bold", and we will see it recurring a lot in the coming months.
The way we read the name ℤ_12 is "the integers mod 12". What does mod 12 mean, you ask? Essentially, we're doing normal addition, except we "cast out" multiples of 12 at the end. That is, 8 + 9 = 17, but then we take away 12 to get 5. A common way you'll see this written in math textbooks is
Note the extra line in the equals sign. Importantly, removing multiples of twelve means that we have
This fact means that we often think of ℤ_12 containing zero as its identity element, and not 12, because they are "the same mod 12."
We're going to do the same thing we did before with S_3 - take a subset H of ℤ_12, and see if we can find a subgroup by choosing elements and then attempting to "close" H. We have to include the identity, which is zero. A natural pick would be to also take 1 - let's see what happens. We have
We want H to be closed, so anything we can get from adding 0s and 1s also has to go into H. Well, today is the day I break the news:
We have to update H to include 2. In another shocking turn of events we have
And, of course, we can keep adding 1 to this until we get all the way up to 11. This trick of "just add one" means that ℤ_12 is cyclic; we'll return to cyclic groups at a later time. One other note about 11 is that it "acts like" negative 1 in ℤ_12: since 12 is like 0, we can see that
This is good as a gut check - it means that we have an inverse for 1, namely, -1. All this to say, choosing 0 and 1 as our starting set doesn't work. Let's try 2 instead:
In the most shocking news yet (truly WWK is the new CNN), we note that
and therefore we have to include 4 in H. Likewise, we have 2 + 4 = 6, 2 + 6 = 8, 2 + 8 = 10, and 2 + 10 = 12 = 0, so we get that
and that H is a proper subgroup!
Summary
Today we covered another foundational notion in the study of groups - that of a subgroup. A subgroup of a group G is simply a subset of G that is also a group under the same operation. As we'll come to see, subgroups are an incredibly important and useful thing to understand when studying groups - they will tell us a lot about the structure of the group.
Next time, we'll come back to our S_3 subgroups which we called H, J, and K. Something is very strange about those three...they're almost too similar.
Exercises
We saw that there is a subgroup of size 6 for the group ℤ_12. What other sizes of subgroup exist? (Don't forget the trivial subgroup and the improper subgroup.)
When we first tried to construct a subgroup of ℤ_12, we started with
H = {0, 1}. The issue we ran into was that 1 generated all of ℤ_12. What other numbers generate ℤ_12? Do you see anything interesting about those numbers in relation to the number 12?
Solutions to Previous Exercises
Choose any permutation in S_3 - that is, any permutation of three elements - and show that it is an injection and a surjection (and, therefore, a bijection).
1. We'll take the permutation (1 2) as our example. We know that (1 2) sends 1 to 2, 2 to 1, and 3 to 3. For (1 2) to be an injection, we need each element we start with to get sent to a different element from all the others - we cannot have 1 and 2 both go to 3, for example. In this case, we see that this is true. For (1 2) to be a surjection, we need every element we end with to have a corresponding input. In this case, we get 2 from 1, 1 from 2, and 3 from 3, so (1 2) is also a surjection. Since (1 2) is an injection and a surjection, it is a bijection.
Think about the groups S_3 and D_6. Do you see any relation between them? Each group has 6 elements - see if you can find some kind of natural "correspondence" between the two.
2. For reasons that will not be apparent until next week, I'm going to hold off on answering this one :).
(Challenging) How many elements are in S_4? What about S_5, and in general S_n?
3. This one is a bit difficult to spot, but there's a trick that solves all of the cases at once. Consider the list 1, 2, 3, ..., n-1, n for any value of n. We want to choose a new permutation of this list. First, we have to choose the first spot. We haven't used any of our numbers, so we have n different choices. For the second spot, we would have n choices, except we can't use whatever we put in the first spot, so we have n-1 choices. This repeats all the way down until we have one spot remaining, and we have to choose whatever is left. That is, S_n has
elements. For S_4, this means we have 4 x 3 x 2 x 1 = 24 elements, S_5 has 120 elements, etc.
If this definition seems fast and loose right now, that’s because it is. I’m not trying to give a formal, rigorous definition of cyclic groups here; rather I just want people to have at least a vague sense of what it is when we introduce it more formally later.


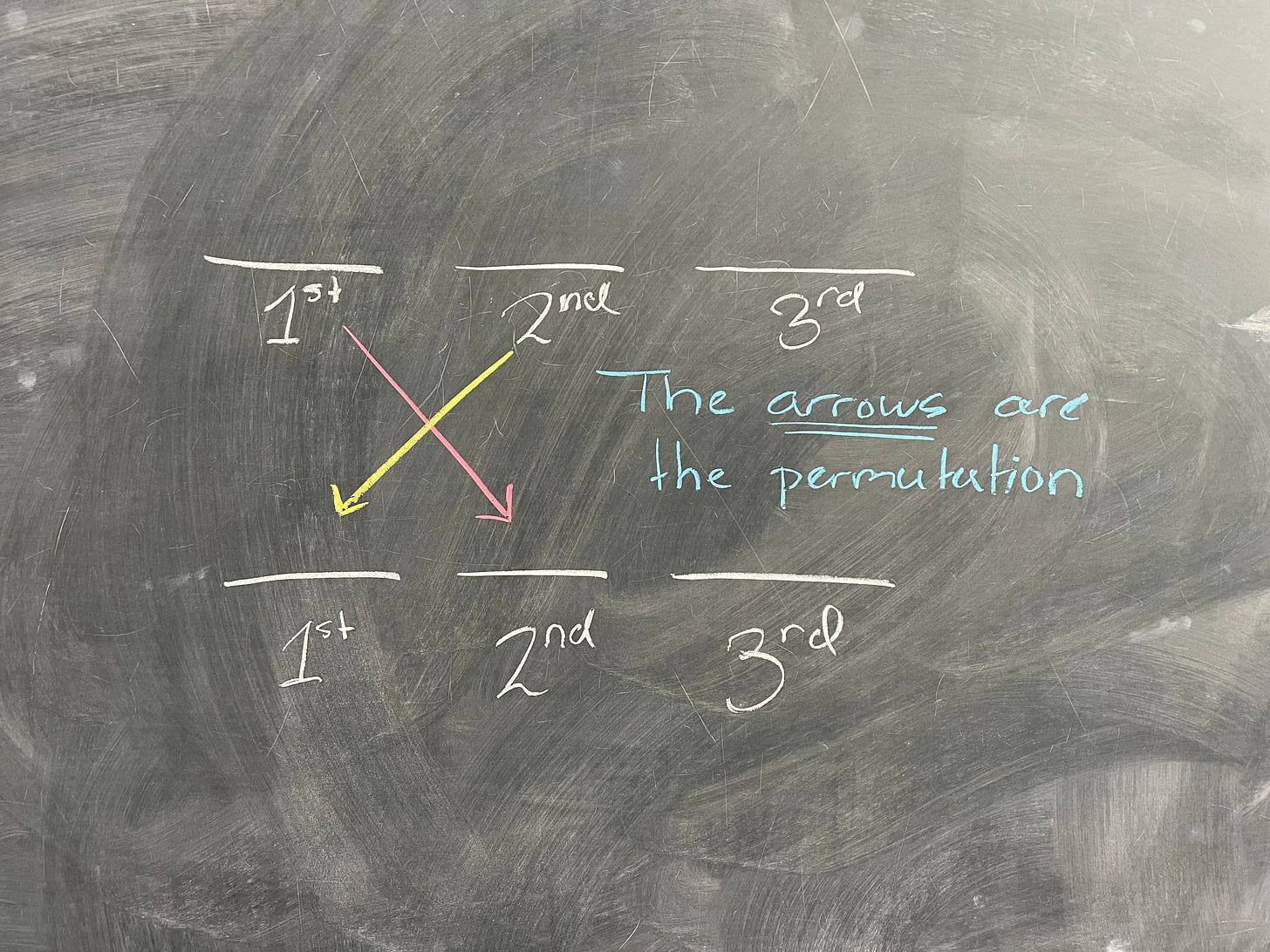
The permutation notation required some mental adjustment for me. Exactly as you said, my mind wants to see it as where the numbers should go (which makes me see (1,2,3) as doing nothing). I had to work through the examples to get it to gel.
The answer to exercise #1 was kind of obvious, but I was a little surprised by the answer to #2.
Good post. Looking forward to more!
great work on explaining the topic! if i could add: on explaining (1 2 3)(1 2 3), if you draw 2 sets of arrows over 3 lines, it'll instantly clear that why the result is (1 3 2).