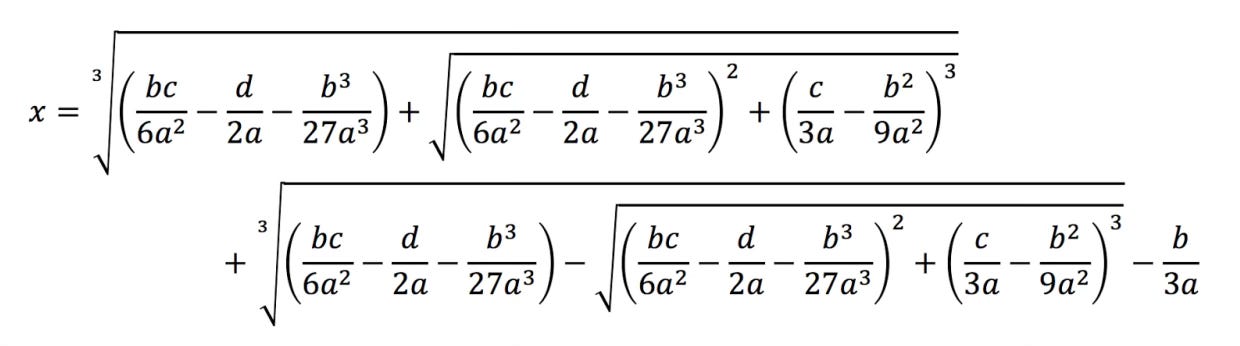The final installment of ITGT! We may return to the fabled lands of group theory one day, but if we do, it will be a different series (likely entitled Finite Group Theorics.) This one is going to be less directly relevant to the larger theme/goal of representation theory, but I think it'll serve as a fun way to cap off the series with something very interesting in its own right. We're gonna define what it means for a group to be simple today, and then we'll finish by talking about the classification of finite simple groups, which is one of the most impressive mathematical accomplishments of the 20th century. The goal of today is to give you a rough sketch of this result, nothing more.
Prime numbers
Before we get to simple groups, I want to go back a bit and talk about something else that I'll be making a liberal analogy to: the prime numbers. You might recall that a prime number is a whole number, say p, such that you can only split it into even piles of 1 or p. For example, 7 is prime, because you can't split 7 things into piles such that every pile has the same amount, unless you have 1 pile of 7, or 7 piles of 1. Likewise, numbers such as 2, 7, 17, and 2003 are prime numbers. But a number like 4 or 6 is not prime, because I can split 4 into 2 + 2, and 6 into 2 + 2 + 2 (and 3 + 3).
Why are primes important? Well, there's a fundamental result in studying the whole numbers called the fundamental theorem of arithmetic, which I will state but not prove here. It says that any whole number can be written as a unique product of primes and powers of primes (up to order), called it's prime factorization.
For example,
and there are no other ways to write 6, up to order. Up to order means we consider
3 ⋅ 2 to be the same as 2 ⋅ 3. Here are some other examples:
So for any whole number n, we can write it as this unique product. In this sense, the primes "build up" all the other whole numbers, because all of them can be written in terms of primes. This fact may seem useless, but it is the basis of a lot of our society today – the first big encryption methods all made extensive use of prime numbers and factorizations. You could think of this like the periodic table of numbers, in a sense. Just like every possible molecule is made up of a combination of elements, carbon, hydrogen, yttrium, etc., so every whole number can be written as a combination of primes.
Why is this relevant, you ask?
Simple Groups
It's relevant because we can ask the same thing about finite groups; namely, is there a unique way we can "break down" a finite group into some sort of constituent parts? Before we answer that fully, let's look at some examples.
Consider the group ℤₚ = ℤ/pℤ, where p is a prime. Recall that Lagrange's theorem says that any subgroup H of a group G must have order that divides G, that is, |G|/|H| must be a whole number. Since ℤₚ has size p, then any subgroup must either be the trivial group or the whole group. ℤₚ does not have any interesting smaller groups "inside" it.
Now turn to consider the group ℤ₁₂. This group has lots of non−trivial proper subgroups; one such subgroup is
Seeing this, you might hazard a guess that there's some way to write ℤ₁₂ as a cartesian product of H (or really, ℤ₄, which is isomorphic to H) with some other group, call it J. Clearly, we need H × J to have 12 elements, so a natural guess would be to take J = ℤ₃. Our guess, then, is that
Is this true? I claim that the function ϕ : ℤ₄ × ℤ₃ → ℤ₁₂ given by
is an isomorphism. Note that ϕ(1, 1) = 1 uniquely determines ϕ, because any element (a, b) of ℤ₄ × ℤ₃ can be written as k(1, 1) for some k. For example,
So what all this means is that the fact that ℤ₁₂ has some normal subgroups is related to the fact that ℤ₁₂ ≅ ℤ₄ × ℤ₃. Notice that 12 = 4 × 3.1 This naturally gives rise to the following definition:
Definition: Let G be a group. We say that G is simple if there are no non−trivial, proper normal subgroups of G. If G is finite and simple, we say that G is a finite simple group.
It's important to point out, based on our previous example, that the analogy between groups factoring and integers factoring is not perfect. You'll notice that, even though ℤ₁₂ ≅ ℤ₄ × ℤ₃, ℤ₄ is not actually simple; the subgroup H = {0, 2} of ℤ₄ is normal, non−trivial, and proper. In our example of the primes, we would be able to further break this down, from 12 = 4 × 3 to 12 = 2 × 2 × 3, because 2 is prime while 4 is not. But here in the land of groups, this is not necessarily the case – ℤ₂ × ℤ₂ × ℤ₃ is not the same group as ℤ₄ × ℤ₃.
Nonetheless, these finite simple groups can be shown to "generate" all the other finite groups in an analogous way.2 What do these finite simple groups look like? Answering that question in full took mathematicians most of the 20th century, and the full proof is around 10,000 pages long. We won't be coming close to that today, but we can get a brief look at it and understand why this is such an impressive accomplishment for humanity.
In fact, though I didn't tell you at the time, we already classified one very important family back in ITGT6 (link). If you recall, we used Lagrange's theorem to show that every group of prime order is cyclic. We already showed, though, that ℤ/pℤ is a simple group as well! What this tells us, then is that the cyclic groups of prime order are an infinite family of finite simple groups.
The Classification Theorem
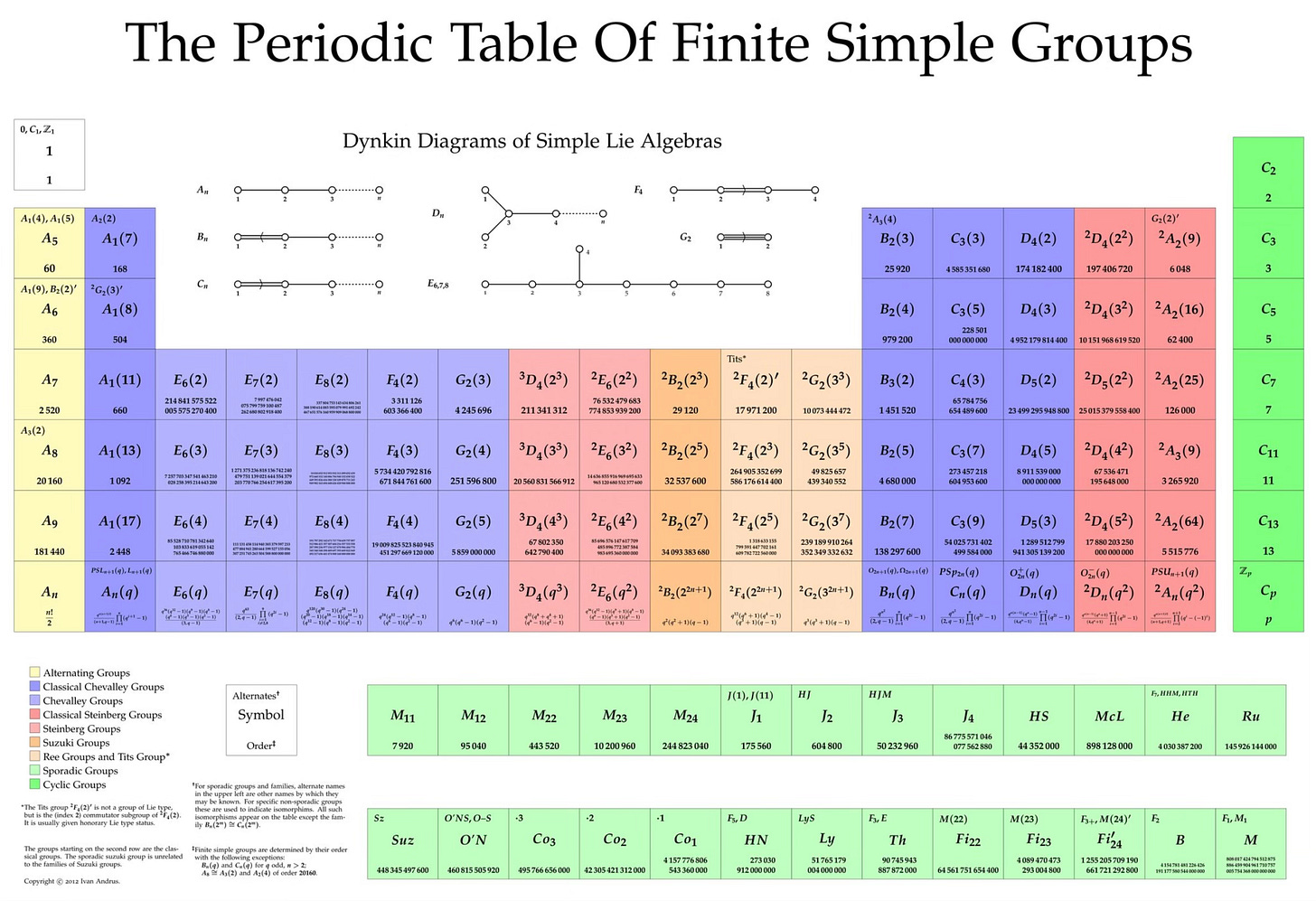
Now, I'm going to state, without proof, the full classification of finite simple groups: I'll explain the new terms after the statement.
Theorem: (Classification of Finite Simple Groups) Let G be a finite simple group. Then G is isomorphic to:
a member of four infinite families, namely:
The cyclic groups Cₚ ≅ ℤₚ of prime order;
The alternating groups Aₙ for n ≥ 5;
The groups of Lie type;
The derived subgroup of the groups of Lie type, such as the Tits group;(footnote: so named after the mathematician Jacques Tits, who had many things named after him.)
or one of the 26 sporadic groups.
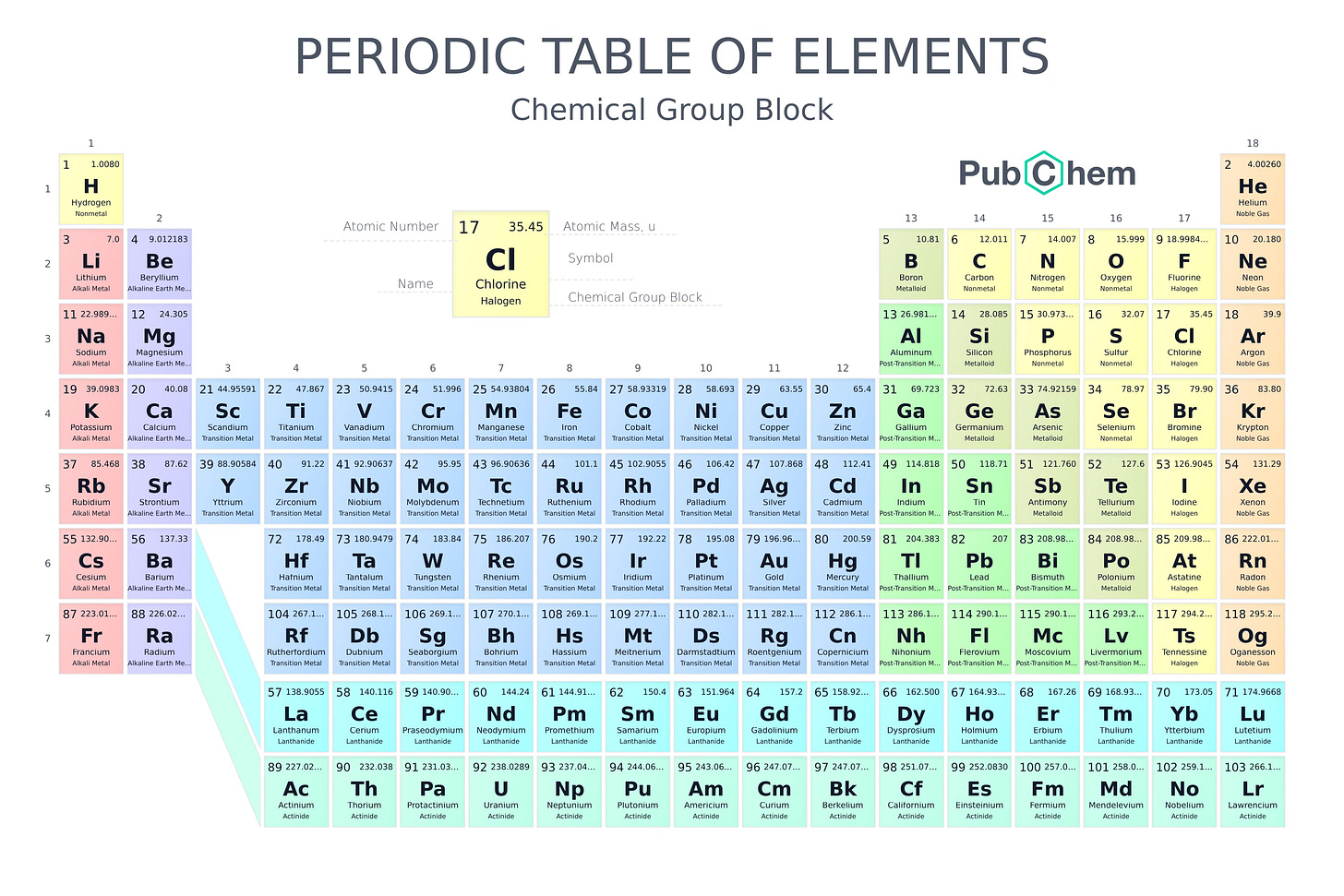
Someone put this information into this wonderful diagram, modeled after the chemical periodic table. It’s worth pointing out that, while there are exactly 18 infinite families, which does line up with the 18 columns of the periodic table of elements, the vertical alignment is not really “true” for groups. It’s just there to make the, admittedly, very odd coincidence, more obvious. On the diagram, we have our familiar cyclic groups as the rightmost column; they are denoted there as C₂, C₃, C₅, etc. These are equivalent to ℤ/2ℤ, ℤ/3ℤ, ℤ/5ℤ, etc. Let's explain, briefly, the new terms.
The alternating groups Aₙ are subgroups of Sₙ; we find these in the leftmost column of the table. There's a natural way in which we can split Sₙ into two sets of equal sizes, called "odd" and "even". The "even" set forms a subgroup, and we call this Aₙ. These are important in some unexpected places. You may recall the quadratic formula from high school algebra, which says that if you have some quadratic polynomial ax² + bx + c, and you want to know what values of x make this equal 0, the answer is
Well, it turns out that there is a similar formula for cubics, which have the form ax³ + bx² + cx + d, and even a formula for quartics, which have the form ax⁴ + bx³ + cx² + dx + e; the reason you are not taught them in school is because they are completely impractical. Even the cubic formula is beyond comprehension:
The weird thing is, there is no quintic formula. That is, for a polynomial of the form
ax⁵ + bx⁴ + cx³ + dx² + ex + f, we have proved that there is no formula for the roots of this. Why is that? Well, the proof requires more math than we can talk about right now, but the reason quintics have no formula while quartics and lower do is deeply connected to the fact that A₅ is simple, while A₁, A₂, A₃, and A₄ are not. Very strange, right?3
Groups of Lie type is really a much larger family; there's lots of different infinite families within this kind, all of which arise from something called matrix groups. If you don't know what a matrix is, don't worry about it; we'll get there relatively soon when we study linear algebra. They are called groups of lie type, because they are finite (non−infinite) analogs of groups called Lie groups. So named after the mathematician Sophus Lie (pronounced Lee), these are groups that also "act" like some kind of mathematical space. For example, the real numbers are a group, but they are also a 1−dimensional, smooth line. Spaces like this (which can be much larger: 2−d, 3−d, indeed any dimension at all) are called manifolds. A Lie group is a group that is also a manifold.
The derived subgroup of a group G is the smallest normal subgroup N so that G/N is abelian. In this sense, if your derived subgroup is quite large, it means G is very far away from being abelian. This family of groups do not have quite the same structure as the groups of Lie type, but they are related to them because they are the derived subgroups of them. In total, there's the cyclic groups, the alternating groups, and then 16 infinite families, either of Lie type, or the derived subgroups of groups of Lie type.
The sporadic groups are precisely the groups that do not fit into any of these 18 infinite families. There are exactly 26 of them, and most of them are related to the biggest sporadic group, which is called the Monster group, or sometimes the Friendly Giant. Denoted by M, we know that
Or, if you prefer an approximation, |M| is around 8 ⋅ 10⁵³. You might recall that originally, the way we introduced groups were that they described symmetries of objects. Well, the smallest object that has M as a symmetry group lives in, not 2−dimensional space like our groups D₂ₙ, nor in 3−d space, but in 196,883−dimensional space. It's massive.
Again, just to reinforce this point, we have proven, without a shadow of a doubt, that that table of finite simple groups describes every possible finite simple group. There are the 18 infinite families, and the 26 sporadic groups, and that's it. No more to be found! If you're like me, you're probably wondering why something like the sporadic groups would ever be useful beyond "hey, this is neat to know." Well, it turns out that M in particular has extremely deep connections to number theory.4 So, even something as seemingly disconnected from other parts of math like the monster group have deep, deep applications.
I could do some long−winded soliloquy on how strange this fact is, that there's exactly 18 infinite families and exactly 26 sporadic groups, but I would be incapable of doing it properly. Instead, you should go watch this numberphile video, wherein John Conway, the man who originally stated the monstrous moonshine conjecture (and named it such) explains his feelings on the monster.
Summary
Today is intended as a quick sketch in the direction of one of the great mathematical results of the 20th century. You should take stock of just how much you've learned already and be proud of it! I'm going to assign some simple homework problems, but these are more optional than the usual, as this article really is meant to be more for enjoyment than work. We're going to move on past group theory for awhile, as our next series will be Rings and Fields. These are, like groups, a kind of algebraic structure, but they have more structure than groups do. We need them to understand our third series, Linear Algebra. I don't expect either of these to be quite as long as this one; my goal is to be able to finish Linear algebra by the end of December.
Exercises
Determine whether the following groups are simple:
ℤ/19ℤ;
D₁₂;
ℤ/2ℤ × ℤ/7ℤ;
S₄.
Find an example of a group G, which has normal subgroups H and K, so that H and K are isomorphic, but G/H is not isomorphic to G/K. (Hint: it might be helpful to consider choices of G where G is a cartesian product of two other groups.)
Let ϕ: G → G' be a group homomorphism, and let N be a normal subgroup of G. Show that ϕ[N] is a normal subgroup of ϕ[G].
Solutions to previous exercises
Let H be a subgroup of G, and let G be an abelian group. Show that G/H is abelian.
Since G is abelian, it is common to use additive notation for the group operation, so we will do so here. Let a + H and b + H be elements of G/H. We want to show that
This follows immediately from how our operation on cosets is defined, which is
Since G is abelian, a + b = b + a, so we can swap those around. Then we have
so indeed, G/H is abelian.
Let G be a group, and a ∈ G. Recall that ⟨a⟩ is defined as the subgroup {aⁿ | n ∈ ℤ}. Determine whether the following factor groups make sense; if they do, compute their order. Remember that order = size = number of elements in the group. So for example, the order of the group ℤ/4ℤ is 4, since it has four elements.
ℤ/7ℤ.
ℤ₁₆/⟨4⟩.
D₈/⟨s⟩.
D₈/⟨r⟩.
Any subgroup of ℤ is normal, so ℤ/7ℤ makes sense. As we’ve seen, this will be the group {0, 1, …, 6} under addition, so it has order 7.
First, note that ⟨4⟩ = {0, 4, 8, 12}. As before, this factor group indeed makes sense, because ℤ₁₆ is abelian and any subgroup of an abelian group is normal. I could give an isomorphism between ℤ₁₆/⟨4⟩ and ℤ/4ℤ, but actually we know that the size of the group is just the size of ℤ₁₆ over the size of ⟨4⟩, which is 16 / 4 = 4.
Since ⟨s⟩ is not normal in D₈, we cannot consider D₈/⟨s⟩ as a factor group.
⟨r⟩ is normal in D₈, since it has index 2; thus D₈/⟨r⟩ has order 2.
What is ℤ × ℤ/⟨(2, 2)⟩ isomorphic to?
The initial guess might be that it’s just ℤ, exactly like the first time we did something like this. However, this is not quite right. First, we need to compute ⟨(2, 2)⟩. This is the subgroup generated by (2, 2), which is
Importantly, we do not have (1, 1) in this subgroup. So, the coset of (1, 1) in
ℤ × ℤ/⟨(2, 2)⟩ is different from the coset of (0, 0) in ℤ × ℤ/⟨(2, 2)⟩! Let’s compute this coset. We have
From this we can see that the important difference between this case and when we factored out by ⟨(1, 1)⟩ is that the line is not really one line, but two lines.
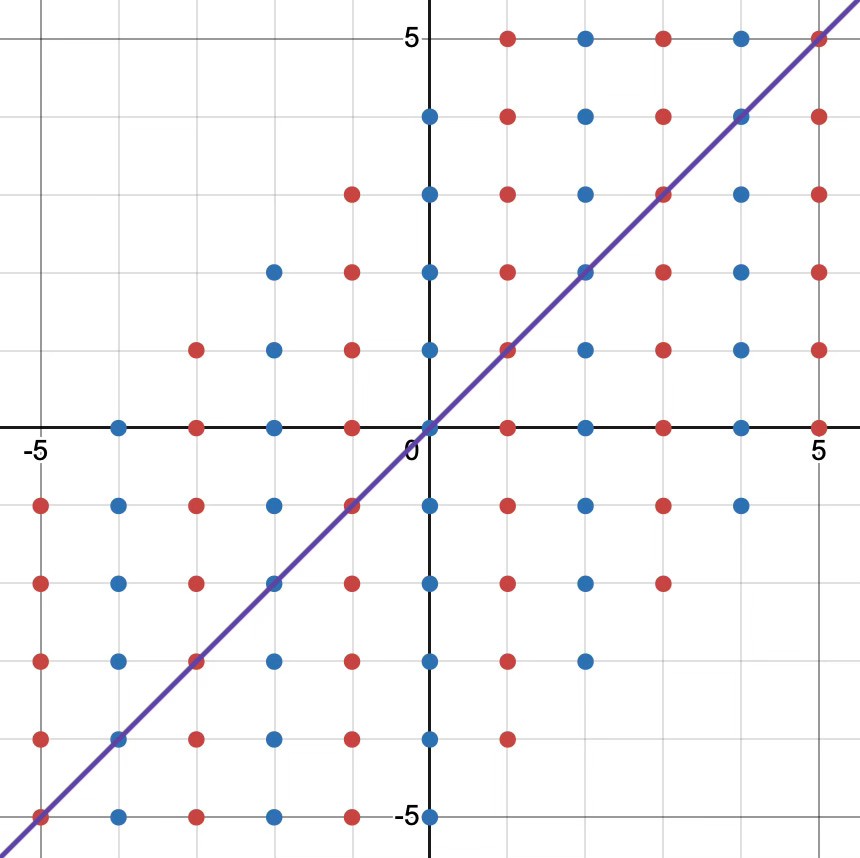
Here, I’ve drawn the one line through the middle as purple, because really, there’s two lines there. You should think of the red dots on the line as one “line” (because they are one coset) and similarly, the blue dots on the line are another coset. Then, just as before, we imagine shifting them up and down and get a natural isomorphism with ℤ. So, our guess for what this might be isomorphic to would reasonably be ℤ × ℤ₂; ℤ because of our previous experience, and the extra factor of ℤ₂ to account for the blue/red difference. Let’s try to construct an isomorphism. Define ϕ : ℤ × ℤ → ℤ × ℤ₂ by
where m₂ is the remainder when m is divided by 2. Then this is a homomorphism (this can be checked easily), and is surjective (why?) so what remains is to compute its kernel. We have
But this is precisely what we want, for this is the set ⟨(2, 2)⟩. Thus by the first isomorphism theorem, ℤ × ℤ/⟨(2, 2)⟩ is isomorphic to ℤ × ℤ₂, as desired.
This does not always work, however. Just because 12 = 2 × 6 does not mean we can factor ℤ₁₂ as ℤ₂ × ℤ₆, unfortunately.
If you're curious about the details, the search term you're looking for is the Jordan−Holder theorem. In particular, where finite groups differ from primes is that a given "composition series" for a group may also be the composition for another, different group.
I’m sort of speaking loosely here; of A₁, A₂, A₃, and A₄, only A₃ and A₄ really make sense. A₁ and A₂ are both the trivial group.
In particular, there's a basic object of study in the realm of modular forms called the j−invariant, and the number 196,883 shows up in the expansion of the j−invariant. For a long time, people thought this was an odd coincidence, but in 1992 a man named Richard Borcherds (who is on YouTube, by the way) proved something called the monstrous moonshine conjecture. He was later awarded the Fields Medal in 1998, in major part because of this result.