Introduction to Group Theory V
A kernel of truth...
Last time, we learned about a concept that will surface again and again on our journey - that of homomorphisms and isomorphisms. If we have two groups, say G and G', and there is a homomorphism φ : G → G’ between them, then we know that G and G' are "similar" in some sense. If φ is an isomorphism, then we know that G and G' are the same, up to the labels. Today we're going to prove some important things about homomorphisms and isomorphisms, and talk about some important concepts relating to them.
Oh, one very important note: where I am living for the next few weeks does not give me easy access to a blackboard, so I have replaced the blackboard with standard-issue Numberphile Brown Paper™ for the time being.
Properties of Homomorphisms
The first thing we're going to do today is talk about some important properties of homomorphisms. These are things that we want to be true, or we think intuitively should be true, so it's all the more important for us to know that they are true. Before we get to these properties, we need a definition:
Definition: Let φ : X → Y be a function, and suppose A ⊆ X and B ⊆ Y (that is, A is a subset of X, and B is a subset of Y). We define
and call it the image of A under φ. (The ∈ symbol here just means "is in" - we read a ∈ A as "a is in A".) Likewise, we define
and call it the preimage or inverse image of B under φ.
Here, and any other time you see ":=", it means "we define this thing on the left to be equal to the thing on the right." So, in this case, we are defining the notation φ[A] to mean "the set of things when you apply φ to each element of A." Likewise, we are defining the notation φ^{-1}[B] to mean "the set of things in A that, when you apply φ to them, you get things in B."
Now we come to our first theorem of today. There are a few things we think homomorphisms "ought to" satisfy, at least if they are as nice as we think they are. We want them to preserve the identity and preserve inverses - if φ(e) is not the identity, for example, then we might have some problems.
Theorem: Let φ : G → G’ be a homomorphism.
If e ∈ G is the identity element, then φ(e) is the identity element e' ∈ G'.
If a ∈ G, then φ(a)^{-1} = φ(a^{-1}).
If H is a subgroup of G, then φ[H] is a subgroup of G'.
If K' is a subgroup of G', then φ^{-1}[K'] is a subgroup of G.
Proof:1 By the homomorphism property, we have
Multiplying both sides of the equation by φ^{-1}(e), we see that
This proves 1. Likewise, we have
which shows that φ(a)^{-1} = φ(a^{-1}) for all a; 2. is now proven. Now we turn to the proof of the latter two claims, which is slightly more difficult.
Let H be a subgroup of G. Because of statements 1 and 2, we know that φ(e) = e' and for any a ∈ H, we have φ(a^{-1}) = φ(a)^{-1}. Since H is a group, we know that it contains the identity and it contains inverses for all its elements, so φ[H] likewise contains the identity and inverses. What remains to be shown is closure (since associativity is inherited from G'.) Let a, b ∈ H. We know that φ(a) and φ(b) are in φ[H]. What we need to show is that φ(a)φ(b) ∈ φ[H]. Since H is a subgroup, we must have ab ∈ H, which means φ(ab) ∈ φ[H]. Because φ is a homomorphism, we have φ(ab) = φ(a)φ(b), so φ[H] indeed contains φ(ab). Thus, φ[H] is a group, and a subgroup of G', so 3. is done.
Likewise, let K' be a subgroup of G'. Recall that
that is, φ^{-1}[K'] is the set of things in G that give you things in K' under φ. We want to show that this (which from here I will denote K) is a subgroup of G. Suppose a and b are in φ^{-1}[K']. Then this means that φ(a) and φ(b) are in K'. Since K' is a group, we have φ(a)φ(b) = φ(ab) ∈ K', which means ab ∈ K; this means that K is closed. One of the exercises for today will be to show why K contains the identity, and why every element in K contains its inverse. Once those are shown, we have completed the theorem. ☐2
An immediate corollary of this theorem is that, if we have a homomorphism φ : G → H, then the image of G under φ is a group. This follows as an application of statement 3, setting H = G. Another reason this theorem is important is because it allows us to make the following definition:
Definition: Let φ : G → H be a group homomorphism. The subgroup
is called the kernel of φ, which we denote ker(φ). Note that we know this is a subgroup of G because of our previous theorem - statement 4 tells us that the preimage of any subgroup of G' is a subgroup of G, and {e'} is a subgroup of G'.
Let's work an example to get adjusted to these new concepts. We'll consider a homomorphism φ : ℤ_12 → D_24. Recall that ℤ_12 is our clock face group, and that D_2n is the symmetry group of a regular n-gon. In this case, we want 2 • 12 = 24, so here n = 12, meaning we need a regular dodecagon3. Let ρ - the Greek letter rho - denote the smallest rotation in D_24.
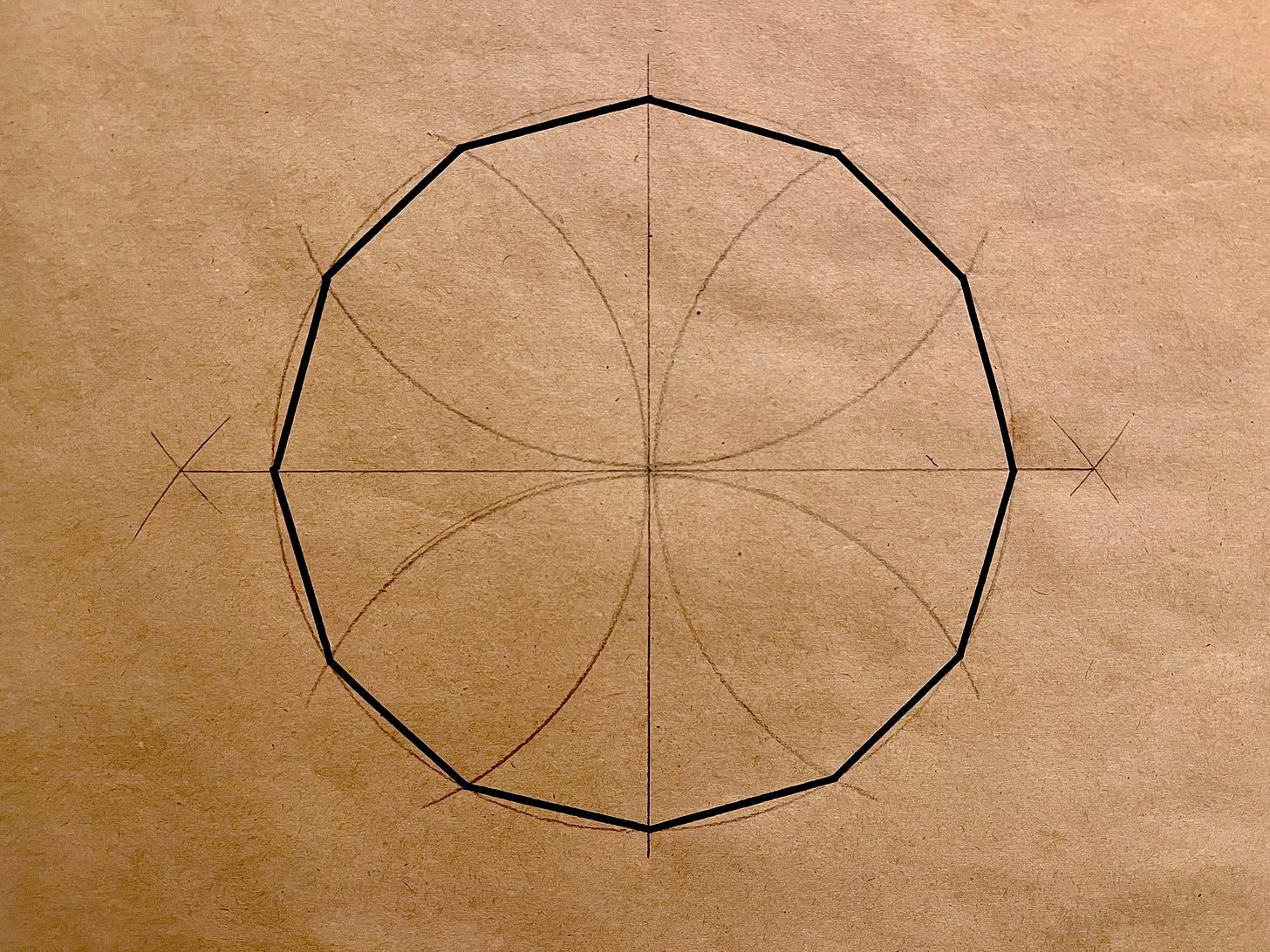
We define φ(k) = ρ^k. We first want to check that φ is a homomorphism. Let a, b ∈ ℤ_12. If a + b < 12, we have
If a + b ≥ 12, though, we have to subtract 12 off. For example, if a = 8 and b = 9, we have 8 + 9 = 17 — we have to subtract 12, because 17 is not on our clock face (or more formally, 17 is not in our set.) 17 - 12 = 5 is, though, so we have
Now, if we think about this carefully, we see that ρ^{-12} is actually just the identity!
So, this means that we have
which is what we wanted. So, φ is indeed a homomorphism. Now we can compute a couple examples of images and preimages. Let A = {0, 3, 6, 9} ⊂ ℤ_12. The image of A under φ is
Not particularly surprising, is it? Let B = {ρ^2, ρ^6, ρ^8} ⊂ D_24. The preimage of B under φ is
which should once again feel intuitive. Lastly, we compute the kernel of φ:
It is interesting to note that the kernel here is trivial. Some might wonder why we can say it’s “trivial” when it clearly contains the identity. Well, any homomorphism must send the identity in the first group to the identity in the second, so the fact that the identity is in the kernel is kinda…trivial. In our case, φ does not send any elements other than the identity in ℤ_12 to the identity in D_24. Along with that, we note that φ is injective.
For one more example, let's consider one of our homomorphisms from last time - we defined φ : ℤ_6 → H, where H was the set {0, 2, 4, 6, 8, 10}. We saw last time that this φ is injective - and indeed we again see that
When relationships like this continue to pop up, it is often good to try to prove them in general. Sometimes, it won't work - there's an example of this we may or may not get to4 in this series on group theory - but just as often, it will work out; and in this case, it does.
Theorem: Let G and G' be groups, and φ : G → G' be a homomorphism. Then φ is injective if and only if φ has trivial kernel - that is, ker(φ) = {e}.
Proof: To prove a statement of this kind - an "if and only if", which commonly gets abbreviated to iff - we must show that each "side" implies the other. In this case, that means we need to show that "φ is injective" implies "φ has trivial kernel", and show "φ has trivial kernel" implies "φ is injective". In formal logic notation, the way you would write this is
Because of this, we often say things like "we prove the forward direction" - meaning that we prove the direction "φ is injective" ⟹ “φ has trivial kernel".
Okay, after all that, we can actually start on the proof now.
(⟹). This is the easy direction. Assume φ is injective. By the definition of injective, if φ(a) = φ(b), then a = b. We know that φ(e) = e'. Choose any element g ∈ ker(φ). We do not know anything about the kernel yet - it could have one element or a hundred, and we're saying g can be any of them. What we want to prove is that we must have g = e. Well, since φ is injective, and φ(g) = e' since g is in the kernel, we must then have g = e. So, the kernel is trivial.
(⟸). For this direction, it's much easier to use a common trick. If you want to prove that p implies q, it is logically equivalent to prove that ¬q implies ¬p - where ¬ just means "not".5 So, we'll be doing this as well - we're going to start with "φ is not injective" and show that "φ does not have trivial kernel."
Assume φ is not injective. This means that there exists some a, b ∈ G such that a ≠ b, but φ(a) = φ(b). Of course, if these are the same, then the inverse of one is the inverse of the other - so we have
But, because of our homomorphism law, we can move the inverse "inside" and then combine the two elements together - which means
Since a ≠ b, this means ab^{-1} ≠ e, which means we now have two elements in the kernel:
There could be more in the kernel, but we don't need anymore - all we needed to show is that ker(φ) contains more than just the identity. ☐
This is a pretty convenient result! It may not seem that helpful, because all of our examples have been with small groups - if you wanted to check that a homomorphism was injective, you could just...check all twelve elements of the domain. But this result holds no matter how big our group is - in fact, it even holds if the groups are infinite.
Summary
Today we furthered our understanding of homomorphisms, defined a couple important tools, and proved some nice theorems:
We defined the image and preimage of a set under a homomorphism;
showed that homomorphisms obey some nice rules, e.g., φ(e) must equal e';
defined the kernel of a homomorphism;
and showed that a homomorphism is injective iff the kernel is trivial.
This is roughly what I expect to be the halfway point in the ITGT series, so if you've made it this far, pat yourself on the back (and don't think too much about how many sections I said are to come after the ITGT series.)
Exercises
In the proof of our first theorem, we left it to the reader to show that K contains the identity and inverses. Show that K indeed contains the identity and inverses.
Using the homomorphism you found last week from D_8 into S_4, compute the images of the sets A = {e, s} and B = {e, r, r^2, r^3}.
Construct a homomorphism from S_3 to S_4 with non-trivial kernel.
Solutions to Previous Exercises
We know that S_3 and D_6 are isomorphic, but the isomorphism we found is from S_3 to D_6. Can you find an isomorphism that's from D_6 to S_3? (Keep in mind that we know an "inverse" function has to exist, since the isomorphism we found is a bijection.)
This one is easy - define φ^{-1} : D_6 → S_3 by "flipping the arrow" - whatever we sent an element of S_3 to in D_6, just send that element of D_6 to the same element of S_3. For example,
etc.
Find a homomorphism from D_8 into S_4.
It's the same idea here as when we did S_3 and D_6: we're going to see what happens to the vertices of our square, and then send them to the corresponding permutation in S_4.
Find a homomorphism from S_3 into S_4.
While I don't think this one is too difficult, it does require a conceptual jump. We're going to send each element in S_3 to the element that does the exact same thing in S_4:

This format of THEOREM: followed by PROOF: is ubiquitous in math textbooks and articles; while I will not use it all the time, I find it is sometimes useful to demarcate where the proof ends.
There are many ways for mathematicians to end a proof - this is one of the more common ones. A very old way, for when you either want to sound pretentious or be sarcastic, is QED - quod erat demonstrandum, what was to be demonstrated.
If you’re curious to see the method I used to create this dodecagon, here’s an excellent video displaying the steps.
The example I’m thinking of here, for those already in the know, is that the converse of Lagrange’s theorem is false.
If you haven’t seen this idea before, it might take a second to see why. If we want to show “P implies Q”, what we’re really trying to prove is that anytime P is true, Q must also be true. Let’s assume that this is true - if P, then Q. Well, what if we know that Q is false? Then P cannot be true - because if P were true, then Q would be true.
There’s another way to prove this fact using truth tables, which you’re free to google if you like, but I find that sometimes students can find that method unsatisfying.



After a re-read, two questions to see if I have this straight:
Given φ: X→Y where A⊆X and B⊆Y, is it fair to state: the image of A is crudely speaking just φ[A] = B, and the preimage of B is likewise just φ⁻¹[B] = A?
Is a kernel then essentially the preimage of {e'}?
>> "What remains to be shown is closure (since associativity is inherited from G'.) Let a, b ∈ H. We know that φ(a) and φ(b) are in φ[H]. What we need to show is that φ(a)φ(b) ∈ H."
Had to go back and review to tackle the current lesson. Should the above end: "...φ(a)φ(b) ∈ φ[H]"? The text continues, "Because φ is a homomorphism, we have φ(ab) = φ(a)φ(b), so φ[H] indeed contains φ(ab)." Which is what made me think so. (I'm apparently finding the concept of a kernel hard to wrap my head around.)