Introduction to Group Theory VII
Normal Subgroups, Part I of...
This article – or rather, this particular topic – has worried me to some extent since the day I decided to start writing. Explaining the details on why we need normal subgroups to be defined the way they are is tricky and difficult work. As such, I will likely give a few more exercises than usual...perhaps even five or six. (Gasp!) Lord help us if I think I have justification for stating seven exercises at the end of this article. This is not because I have some sort of twisted sense of humor; rather, I know that if my explanation is less helpful than usual (which it is at least somewhat more likely to be today than on other occasions, I think), then you, the reader, doing exercises, will serve as a much more valuable supplement than usual. And, if nothing else, you are always more than welcome to use the comment section to ask questions where my explanatory ideas failed me. As always, the definitions list can be accessed here if you need to remind yourself of what a term means.
Kernels are normal
Let's start with a quick refresher. A subgroup H ≤ G is normal if, for all g ∈ G, we have
That is, H is normal if, given any g ∈ G, the left coset of H by g is the same as the right coset of H by g.
We've already seen one condition for H being normal. Clearly, if G is abelian, then gH = Hg, because gh = hg for any h ∈ H. There can, of course, be non−abelian groups which have normal subgroups, though; really what normality is saying is that we need all g ∈ G to satisfy
for some values of h₁, h₂ ∈ H. Abelian groups are the special case when h₁ = h₂. Let's see another condition whereby we can know that a subgroup is normal.
Theorem: Let G and G' be groups, and ϕ : G → G’ be a homomorphism. Then the left and right cosets of ker(ϕ) are the same – that is, ker(ϕ) is normal. Furthermore, a and b are in the same coset of ker(ϕ) if and only if ϕ(a) = ϕ(b).
Proof: We first assume that a and b are in the same left coset of ker(ϕ) and show that they must also be in the same right coset. Recall that a and b being in the same left coset is equivalent to a⁻¹b ∈ ker(ϕ). This is because
means b = ak for some k ∈ ker(ϕ), and multiplying on the left by a⁻¹ gives a⁻¹b = k ∈ ker(ϕ). Then ϕ(a⁻¹b) = e'. Because ϕ is a homomorphism, we see that
Therefore we also have
which means that ab⁻¹ ∈ ker(ϕ). Thus, ab⁻¹ ∈ ker(ϕ), which means they are in the same right coset as well. Note that, in the process of this proof, we showed that if a and b are in the same coset of ker(ϕ), then ϕ(a) = ϕ(b). The proof that right cosets imply left cosets here is very similar, and is left as...an exercise to the reader. (Just start by assuming ab⁻¹ ∈ ker(ϕ) and work your way backwards.) This shows that ker(ϕ) is normal in G, since it's left and right cosets are the same.
Now, assume that ϕ(a) = ϕ(b). Then we have
thus a⁻¹b ∈ ker(ϕ). Of course, we could also use b⁻¹a to show that b⁻¹a ∈ ker(ϕ), which means they are in the same left coset and the same right coset. Thus, ker(ϕ) is normal, and a and b are in the same coset of ker(ϕ) iff ϕ(a) = ϕ(b), as desired. ☐
An immediate corollary of this is that if we have a homomorphism ϕ : G → G', then ϕ is injective if and only if ker(ϕ) = {e}.
Proof: First, assume ϕ is injective. Then we know that ϕ(e) = e', and we cannot have any other element g ∈ G satisfy ϕ(g) = e' (since ϕ is injective), thus ker(ϕ) = {e}.
Now, assume that ker(ϕ) = {e}. Every coset of ker(ϕ) has precisely one element. Suppose that ϕ(a) = ϕ(b). By the preceding theorem, since ϕ(a) = ϕ(b), we must have a and b in the same coset of ker(ϕ), which means a = b. Thus, ϕ is injective. ☐
Let's see some examples of this. Consider the homomorphism ϕ : D₆ → ℤ₂ given by
That is, essentially we're detecting if g contains our reflection s or not. If it does, we send it to 1, if it doesn't, we send it to 0. (Check that this is a homomorphism − it may help to remember that rs = sr², and r²s = sr.) Then our kernel is the subgroup H = {e, r, r²}. We saw last time that H is normal in D₆, and indeed this reflects the fact that all kernels of homomorphisms are normal subgroups.
Back to the weirdness...
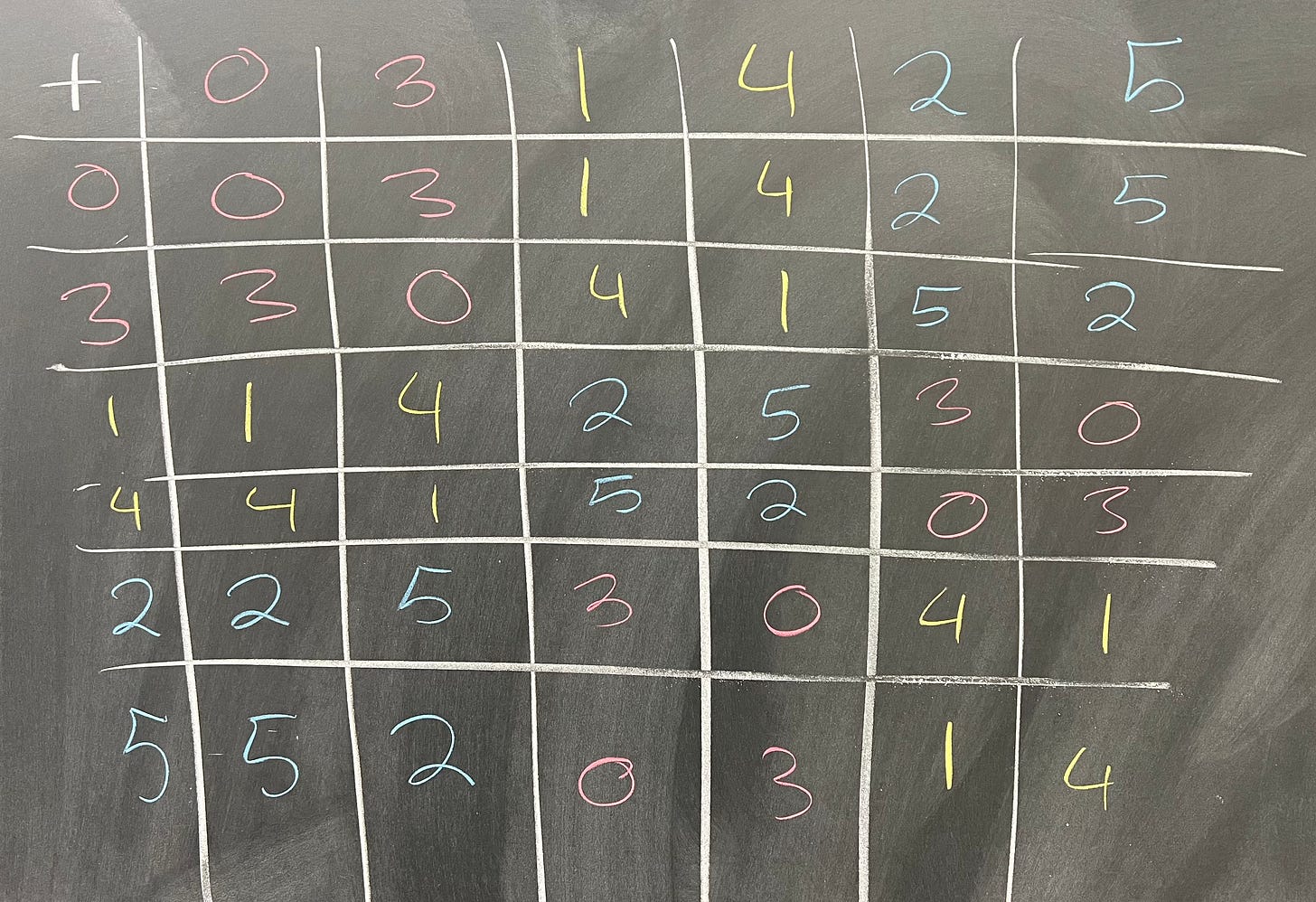
You should recall from last time that when we arranged the addition table for ℤ₆ according to the cosets of {0, 3}, we got something that looked suspiciously like the table for ℤ₃:
In fact, it's pretty easy to find a homomorphism from ℤ₆ to ℤ₃ which has kernel {0, 3}. So what this tells us is that we can define a group operation on the cosets of {0, 3}, which works like:
Let's figure out what exactly we need for this kind of idea to work in general. Let G be some general group and H a subgroup in G. In our example with ℤ₆, we have that the coset {1, 4} plus the coset {2, 5} is the coset {0, 3}. What this boils down to saying is that if I pick any element in {1, 4}, and any element of {2, 5}, and I add them together, I will always get something in {0, 3}. Checking this by hand, we see that:
1 + 2 = 3 ∈ {0, 3};
1 + 5 = 0 ∈ {0, 3};
4 + 2 = 0 ∈ {0, 3};
4 + 5 = 3 ∈ {0, 3}.
So, in essence what we're trying to do here is divide G into some collection of cosets, and then think of the cosets as my new group elements. We want to define an operation (that hopefully, acts "in agreement" with the operation on G) so that these sets of elements of G can behave like elements themselves. Essentially, in this example with ℤ₆ and ℤ₃, what we're saying is that 0 and 3 both "act like" the 0 in ℤ₃, 1 and 4 both "act like" the 1 in ℤ₃, etc.
Another way of saying this is that we want the colors to always add to the same thing. In this picture, we always have Red + Yellow = Blue: (EDIT! I am bad at numbers – note that it should be Red + Yellow = Yellow, not Blue! 0+1 = 1, of course.)
So if I think of my group elements as just the colors Red, Yellow, Blue, I have a well-defined group operation. Notice that the color “Red + Yellow” is not an element itself; it must be equal to either Red, Yellow, or Blue.
Now we'll turn to an example where this doesn't work. Let's take our group D₆ and arrange the group table according to the left cosets of the subgroup {e, s}:
Note that I have written this table such that we are doing (column label) • (row label). So in the third column on the second row, we get r ⋅ s, because r is the column label and s is the row label. Unfortunately, we cannot get a group operation on the cosets of {e, s}: for example, when we take {r, rs} and try to "multiply" it by itself, we get:
r ⋅ r = r² ∈ {r², r²s};
rs ⋅ r = r ⋅ sr = r ⋅ r²s = s ∈ {e, s}.
We could do the others, of course, but already we've failed! We get elements in two different cosets. This means we can't say that {r, rs} ⋅ {r, rs} = {e, s}, because r⋅r ∉ {e, s}, etc.
In other words, this time our colors do not play nicely together. For example, let’s take the red coset and the yellow coset. We get:
Again, we’re considering our only group elements to be Red, Yellow, Blue. So, to define an operation, we have to have Blue + Yellow being equal to one of those three. But, as we can see, when we add Blue and Yellow, we get some red things and some yellow things – which means we can’t say Blue + Yellow = Red, or Blue + Yellow = Yellow, because neither of those statements is always true.
So our condition is as follows:
Definition: Let H be a subgroup of G. If, for all cosets aH and bH of H, and all a₁, a₂ ∈ aH, b₁, b₂ ∈ bH, we have
for some c ∈ G, then we can say that (aH)(bH) = cH. This operation on the left cosets of H is induced by the operation of G; we say that the operation of G induces an operation on left cosets of H. In this case, we may write
to mean that the product of any element in aH with any element of bH must be in the left coset (ab)H.
Think of these cosets aH and bH as the colors from before. We want to define an operation on our set of colors, so that “adding” two colors always gives us the same color. As we’ll see, getting the same color every time is equivalent to this condition that H is normal.
We can actually reduce this slightly by noting the following. Let a₁, a₂ ∈ a₁H and b₁, b₂ ∈ b₁H. Note that this means a₂ = a₁h and b₂ = b₁ j for some h, j ∈ H. Since H contains the identity, we have a₁b₁ ∈ (a₁b₁)H. Let's also assume that a₂b₂ ∈ (a₁b₁)H. This means that a₂b₂ = a₁b₁k for some k ∈ H. From this we see that:
a₁b₂ = a₁(b₁ j) = (a₁b₁)j ∈ (a₁b₁)H;
a₂b₁ = a₂(b₂ j⁻¹) = (a₂b₂)j⁻¹ = (a₁b₁)kj⁻¹ ∈ (a₁b₁)H.
So, we can get rid of some of our conditions from before, and note that to induce the operation on cosets, we just need a₁b₁, a₂b₂ to be in the same coset of H.
Let's do an example. If you did the exercises from last time, you computed the cosets of 5ℤ in ℤ:
0 + 5ℤ = {..., −10, −5, 0, 5, 10, ...};
1 + 5ℤ = {..., −9, −4, 1, 6, 11, ...};
2 + 5ℤ = {..., −8, −3, 2, 7, 12, ...};
3 + 5ℤ = {..., −7, −2, 3, 8, 13, ...};
4 + 5ℤ = {..., −6, −1, 4, 9, 14, ...}.
Using our color analogy from before, we can think of these five cosets as five different colors, and we want to make sure that adding two colors always gets us the same color out. In our mathematical terms, we now want to induce an operation on these cosets. Let a₁, a₂ be in the same coset – that is, let them have the same color – and similarly with b₁, b₂. Then a₂ = a₁ + 5r for some r ∈ ℤ, and similarly b₂ = b₁ + 5s for some s ∈ ℤ. Thus we have:
This means that indeed, the addition operation induces an operation on the cosets of 5ℤ in ℤ. I'm going to do something slightly strange, so that we can see exactly what we required for this to work: instead of writing 5r and 5s, I'm instead going to write h₁ and h₂, and say H = 5ℤ. This gives us:
If you stop and process through this for a moment, you'll see that every step we did works in all groups except for one. We went from h₁ + b₁ to b₁ + h₁ – the whole proof hinges on that. Except, we don't need it to be this strong. In this case, this is precisely true because ℤ is abelian. However, this would work just as well if, say, we had h₁ + b₁ = b₁ + h₃, for some other h₃ ∈ H. This works because, if h₁ + b₁ is Red, then b₁ + h₃ must also be Red. All we care about is that the colors stay the same. Thus, our condition is not that the group is abelian; we just need that b₁ + H = H + b₁. Make sure you see the logic here – all we need is to end up with something that is in H on the right – something with the same color – it doesn’t matter if it’s equal to what we started with. Thus, our condition for inducing an operation on the cosets of a subgroup is precisely that H is normal.
(Note that I miswrote c₁ + 5ℤ as c₁ + ℤ, twice; I’m bad at writing.) In our color language, we don’t need b₁ + 5s to be equal to 5s + b₁ – we just need them to be the same color. But colors are the same as cosets, so what we need is for b₁ + 5ℤ = 5ℤ + b₁.
One more example, just to really work through the details here: the cosets of 4ℤ in ℤ are
0 + 4ℤ = {..., −8, −4, 0, 4, 8, ...};
1 + 4ℤ = {..., −7, −3, 1, 5, 9, ...};
2 + 4ℤ = {..., −6, −2, 2, 6, 10, ...};
3 + 4ℤ = {..., −5, −1, 3, 7, 11, ...};
We want to be able to define an operation on ℤ/4ℤ, which is how we denote the set of cosets of 4ℤ in ℤ. (So, our immediately previous example would be denoted ℤ/5ℤ – the set of cosets of 5ℤ in ℤ.) To do so, we need to make sure that if I pick some h₁ + 4ℤ and I add every element in that set to every element in some other h₂ + 4ℤ, then everything I get needs to be in the same coset. If one element is in h₃ + 4ℤ and another is in h₄ + 4ℤ, then we have a problem, because then our addition isn't well defined. So, let’s let a₁, a₂ be in the same coset of 4ℤ and b₁, b₂ be in the same coset of 4ℤ. Then what we want to show is
If this is true, then our induced operation is indeed well−defined. How can we show this? Well, we know that a₂ = a₁ + h and b₂ = b₁ + j, where h and j are in 4ℤ. So we have
What we really want, from here, is to get that h and j together. Now, in this case we again know that h and b₁ are in an abelian group, so h + b₁ = b₁ + h. But again, all we care about is that we get a₁ + b₁ plus something in 4ℤ. It doesn't matter what it is! We just need the operation to work on the cosets. So, we can say that to satisfy this, we just need h + b₁ = b₁ + k, where k is some other element in 4ℤ. But of course, this just means that b₁ + 4ℤ needs to be the same coset as 4ℤ + b₁, which is our definition of normal.
Was that difficult? Yeah, me too. I would highly recommend pausing for a second, letting it sink in, seeing where you aren't quite sure; maybe even write some things down and make sure it all makes sense. This was a harder thing for me to learn when I first learned this, so if you're struggling, that's common! Please make liberal use of the comment section if you have questions.
What all of this builds up to say is that the normal subgroups of a group G are precisely the subgroups where we can induce an operation on the cosets of the subgroup. This is where we'll start next time.
Summary
We talked today about a concept that a lot of students, myself included, have struggled with – that of normal subgroups. This is building towards something we'll define next time, although we've already used it often today, called a factor group. Essentially, factor groups are given by this process of "grouping together" elements of a group and seeing that collectively, those sets "act like" some smaller group. Think of the ℤ₆ → ℤ₃ example.
I'm going to do something that is very typical for math professors to do, which is also slightly evil; I'm going to introduce a new concept – don't worry, it's not too hard, I promise – in the exercises. Please do exercises 4, 5, and 6, or at least have a go at them!
Exercises
Go back to the proof that the kernel of a homomorphism is normal, and show that assuming a and b are in the same right coset of ker(ϕ) implies that they are in the same left coset.
Find a homomorphism ϕ : ℤ₆ → ℤ₃ with kernel H = {0, 3}.
Find an isomorphism ϕ : ℤ/nℤ → ℤₙ, where ℤ/nℤ is the set of cosets of nℤ in ℤ.
Let G₁ and G₂ be groups. Define the cartesian product G₁ × G₂ to be the set of pairs (g₁, g₂), where g₁ ∈ G₁ and g₂ ∈ G₂. Then we can define a group operation on G₁ × G₂ by
\((g_1, g_2) \cdot (h_1, h_2) = (g_1 h_1, g_2 h_2).\)That is, we're doing the group operation "coordinate−wise". Show that G₁ × G₂ is indeed a group under this operation. (An example of this cartesian product would be ℤ₂ × ℤ₂: it would have elements (0, 0), (0, 1), (1, 0), and (1, 1).)
Let G₁, G₂ be groups. Let π₁ : G₁ × G₂ → G₁ be defined by π₁(a, b) = a, and let π₂ : G₁ × G₂ be defined by π₂(a, b) = b. Show that π₁, π₂ are homomorphisms. (These are called the canonical projection maps, because we're "projecting" our larger group G₁ × G₂ onto G₁ or G₂.)
What is the kernel of π₁, and what is the kernel of π₂?
Solutions to Previous Exercises
Compute the cosets of 5ℤ = {..., −10, −5, 0, 5, 10, ...} in ℤ. Make sure you understand why the left and right cosets have to be the same!
The left and right cosets must be the same because ℤ is an abelian group. We have
0 + 5ℤ = {..., −10, −5, 0, 5, 10, ...};
1 + 5ℤ = {..., −9, −4, 1, 6, 11, ...};
2 + 5ℤ = {..., −8, −3, 2, 7, 12, ...};
3 + 5ℤ = {..., −7, −2, 3, 8, 13, ...};
4 + 5ℤ = {..., −6, −1, 4, 9, 14, ...};
Find a subgroup of D₈ that does not have the same left cosets as right cosets, that is, find a subgroup of D₈ that is not normal.
Unsurprisingly, the same idea that worked for D₆ works for D₈, too: let H = {e, s}. Then we have
rH = {r, rs};
Hr = {r, sr} = {r, r³s}.
Thus, the left coset rH is not the same as the right coset Hr.
Let G be a group with order 48. What are the possible orders of subgroups of G?
By Lagrange's theorem, any order of a subgroup must divide the order of the group. Thus, the possible orders are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.


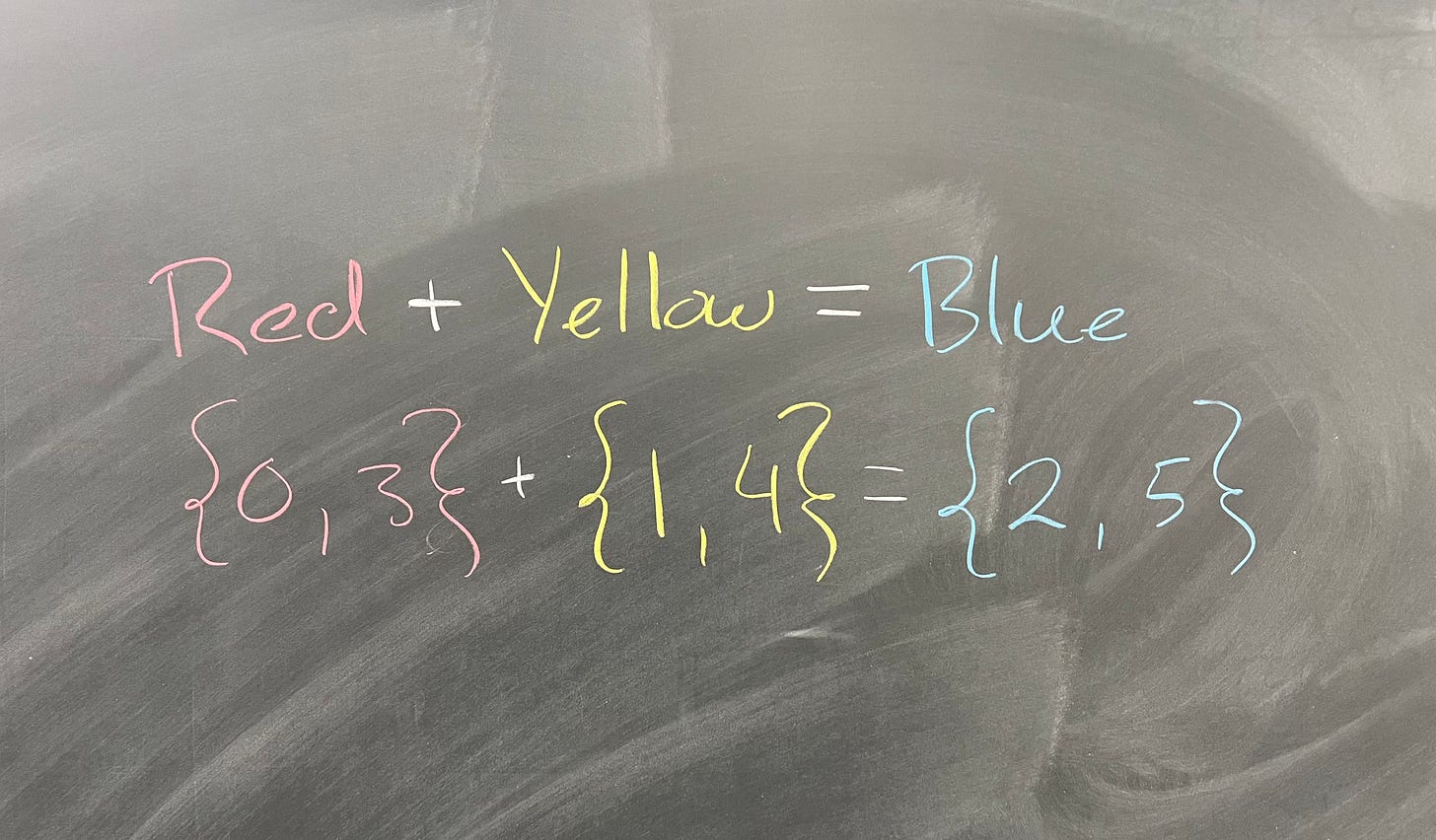

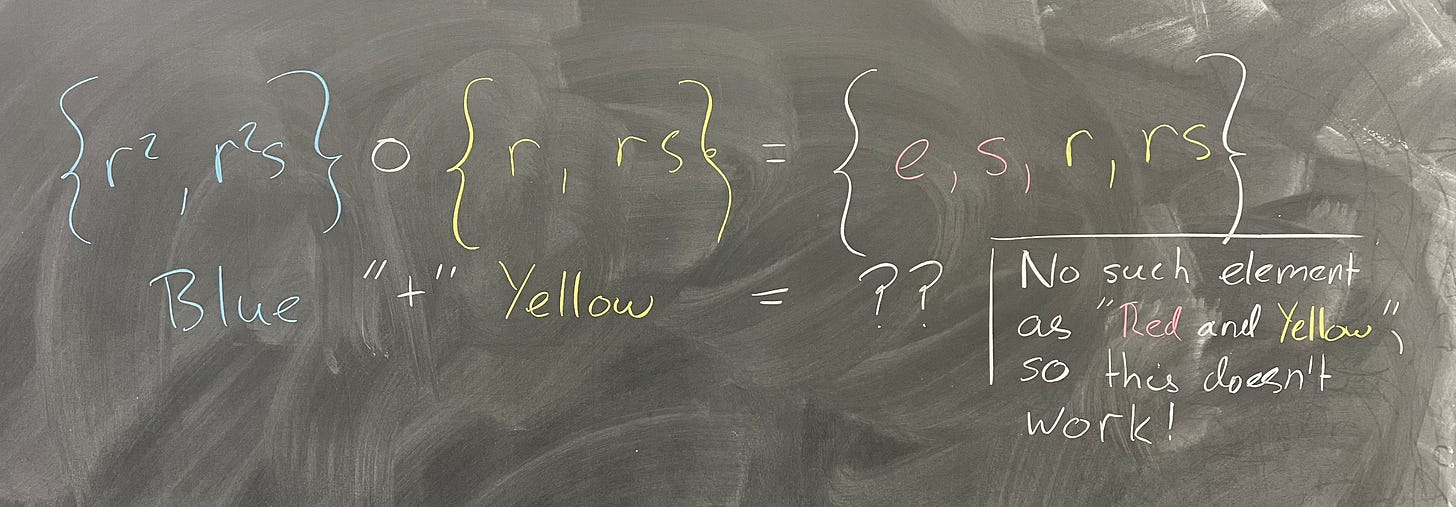
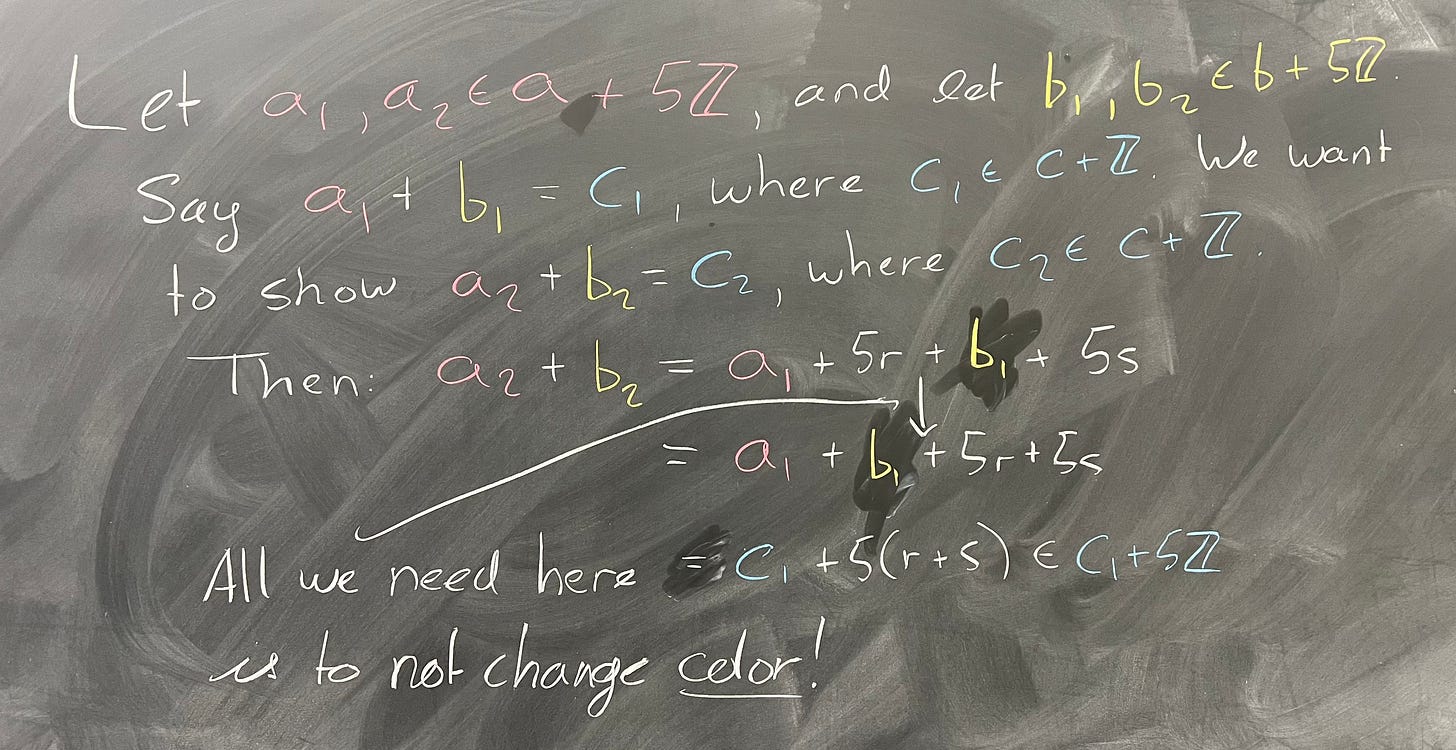
On exercise #3, it's just to *find* an isomorphism? I tried to apply the (a₂ + b₂ = a₁ + h + b₁ + j) equality but got stuck because ℤ/nℤ consists of cosets as members of a set, and we don't seem to be talking about cosets of cosets. Or am I missing something? The isomorphism part seems pretty easy, so I feel like I might be.
I had a cool Cartesian group for #4, and everything was great until #6. My G₁ and G₂ aren't themselves groups, which made finding the kernel problematic. 😁 Back to the drawing board.
A lot of meat on this bone! It's going to take me a few days to chew through this. Everything reads good at first read-through, and I'm looking forward to digging into it. After my coding binge, I'll have to do a little memory refreshing. Feels like a long time since I've done this stuff...