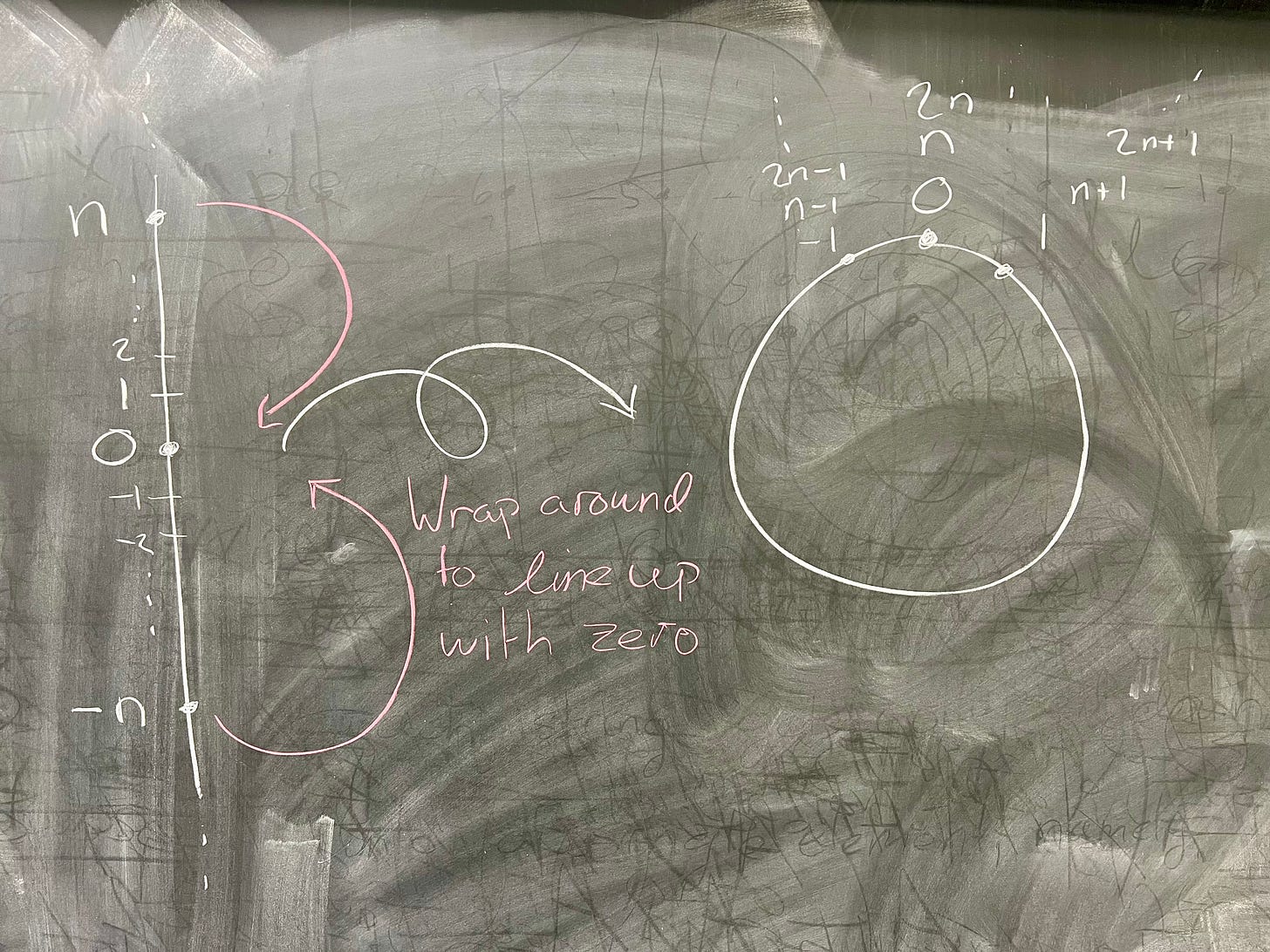Last time, we talked about normal subgroups of groups, and in particular, how the cosets of a subgroup H act like "colors". If H is normal, then we can define an operation on the cosets that gives us a group. I mentioned at the end that today, we're going to define what a factor group is, but actually you've already sort of seen the definition – it's just the induced operation on the cosets. Today, we'll explore factor groups in more detail.
Factor Groups
Recall from last time that a subgroup H is normal if the right cosets of H are the same as the left cosets of H; that is, gH = Hg. We saw that H being normal is precisely the condition we need to think of the cosets as "colors" that we can induce a group operation on – normality is needed for our operation to make sense. Now that we've seen this, we can formally define this notion of a "group of cosets".
Definition: Let H be a normal subgroup of G. Then the cosets of H form a group, which we denote G/H, under the binary operation (aH)(bH) = (ab)H. Here, the operation is the induced operation that we defined last time. This group is called the factor group or quotient group of G by H. (You might also see mathematicians say "G mod H", which works by abuse of language: for an excellent introduction to modular arithmetic, from whence the terminology comes, see this excellent article.)
When we "mod out" by some normal subgroup H, we're essentially saying we want everything in H to "act like" the identity. This makes sense, because our identity element in G/H is the coset eH = H.

Let's see some examples of this, which we've already used a bit, albeit under the rug. Since ℤ is abelian, any choice of n will make nℤ a normal subgroup of ℤ. (Note that we could think of nℤ as ⟨n⟩, the cyclic group generated by n, since n will generate nℤ.) This means that ℤ/nℤ is a well−defined group, since nℤ is normal in ℤ. Keep in mind that we're essentially saying that any element nk is now going to "act like" zero, since our identity element in ℤ/nℤ is the entire coset nℤ.
Given any m, we know that we can express m = nq + r, for some choices of q and r, so that 0 ≤ r < n. (This is a fancy way of saying that you can divide m by n, and your remainder will be r, which can be anything from 0 up to n − 1.) Then we have m ∈ r + nℤ, (note that r + nℤ is a coset of nℤ – one of our "colors") which means
Recall here that ≅ means "isomorphic" – there's a very clear isomorphism between these two groups. Define ϕ: ℤ/nℤ → ℤₙ by
Clearly this is a homomorphism, and moreover it's a bijection, thus it's an isomorphism. (If you aren't sure of these things, check them yourself!)
One way you could think about this coset operation is, once you know that the operation on your "colors" are well−defined, you can pick an element of each color to represent that color. This is exactly what we're doing when we go from ℤ/nℤ to ℤₙ. 0 in ℤₙ corresponds to the coset 0 + nℤ – in other words, 0 is the representative for that coset. Similarly, 1 in ℤₙ is the representative for the coset 1 + nℤ in ℤ/nℤ.
Now we'll turn to computing some easy examples of these factor groups. What's G/{e}? Well, each coset g{e} is just the coset {g}, so the homomorphism ϕ : G → G/{e} defined by
is injective, since ker(ϕ) = e, and surjective, since g ↦ {g} for any g ∈ G. (Check that it's a homomorphism.) Therefore, since it's a bijective homomorphism, this is an isomorphism, so G ≅ G/{e}. This should make sense, since every element gets its own coset. We haven't changed the group. Whenever we have G/H, one way to think about this group is that everything in H now "acts like" the identity. If we mod out by {e}, then, well, we haven't said anything new – no new elements of G now "act like" e.
Likewise, consider G/G. Intuitively, we're setting all of G to be "acting like the identity", so we should expect this to be isomorphic to the trivial group {e}. Indeed, there is only one element of G/G, that is, G itself; therefore it is the trivial group. This is why we have words to specify proper, nontrivial subgroups – if we just say "Let H be a normal subgroup", the factor group we get out may be boring, i.e., either the trivial group or all of G.
We've seen that if we have some homomorphism ϕ : G → G', then the kernel ker(ϕ) is a normal subgroup of G. It is therefore natural to wonder: is every normal subgroup the kernel of a homomorphism? You might already see the answer – and indeed the answer is yes.
Theorem: Every normal group H of a subgroup G is the kernel of some homomorphism ϕ : G → G'.
Proof: Let H be normal in G, G’ = G/H, and let ϕ : G → G/H be defined by
Then we have
so ϕ is a homomorphism. Moreover, the identity element in G/H is H itself, so
From this it is obvious that this occurs if and only if g ∈ H. (If g is not in H, then g⋅e = g ∉ H, which means gH ≠ H.) Thus, H = ker(ϕ). ☐
Since every kernel of a group homomorphism is a normal subgroup, and every normal subgroup can be found as the kernel of a group homomorphism this gives us an alternate definition of normal subgroups.
Definition: Let G be a group and H a subgroup of G. We say H is normal if H = ker(ϕ) for some group homomorphism ϕ : G → G'. This is equivalent to our first definition of normal.
This isn't any new information − it's just giving you an alternate framework for thinking about normal subgroups. Yes, they can be characterized as gH = Hg for any g, but they can also be characterized as precisely the kernels of group homomorphisms.
The First Isomorphism Theorem
We now have all the tools we need to state and prove one of the most powerful theorems in the study of groups: the First Isomorphism Theorem. There are three or four Isomorphism Theorems, depending on who you ask; we'll only need the first one for our purposes. (Note here that if f and g are functions, then we let (f∘g)(x) = f(g(x)). We use ∘ to denote the composition of these functions.)
Theorem: (The First Isomorphism Theorem) Let ϕ : G → G' be a group homomorphism, with kernel H. Then ϕ[G] is a group, and μ : G/H → ϕ[G] given by μ(gH) = ϕ(g) is an isomorphism. If γ : G → G/H is the homomorphism given by γ(g) = gH, then ϕ(g) = (μ ∘ γ)(g).
Proof: We showed in ITGT5(link) that ϕ[G] is a subgroup of G'. We know that the kernel H is normal, so μ is well−defined. We must now show μ is a homomorphism. Let aH, bH ∈ G/H. Then
Since ϕ maps G onto ϕ[G] (that is, ϕ is surjective on ϕ[G]), we know that μ is surjective. (Stop and pause for a moment to make sure you see the logic here!) To show that μ is injective, we compute its kernel. We have
But we know what the kernel of ϕ is – it's H. So we need gH = H, which is precisely the condition g ∈ H. Thus, H is the only element in G/H with ϕ(g) = e, so ker(μ) is trivial. Therefore μ is injective. We showed that a homomorphism is injective iff it has trivial kernel in ITGT5 as well – refresh there, if you need to.
Now we turn to the latter part of the theorem – showing that ϕ(g) = (μ ∘ γ)(g). We have
Thus they are equal. ☐
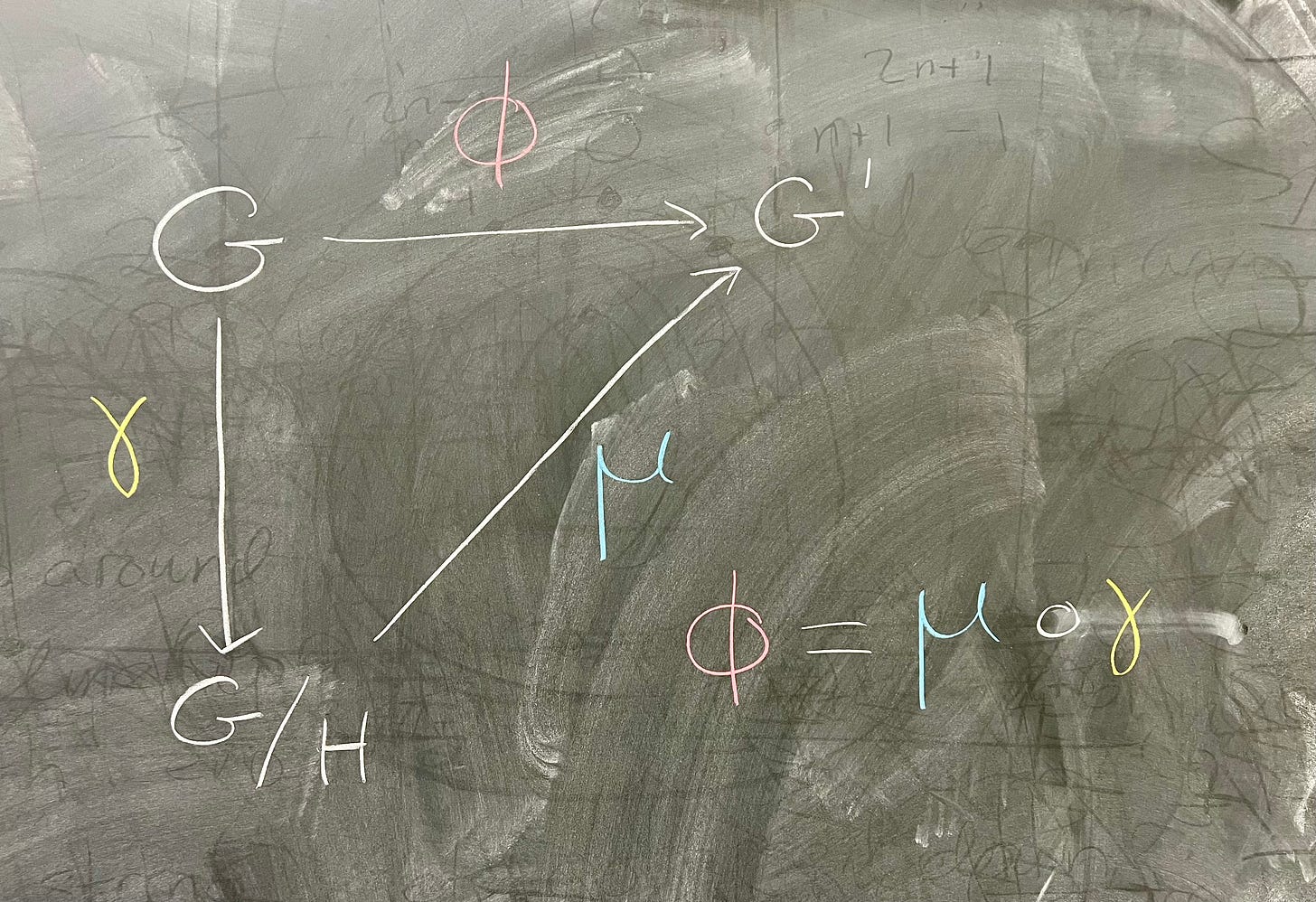
Really, what's important about the First Isomorphism Theorem is that it tells you, for any group homomorphism ϕ : G → G', we always have
We'll do some examples of computing factor groups using this theorem, but before we get there it'll be useful to cover one of the definitions I gave last time in the exercises.
Definition: Let G₁ and G₂ be groups. The cartesian product G₁ × G₂ is the set of ordered pairs
It is a group under the operation given by
Lets look at an example of a cartesian product. Let G₁ = G₂ = ℤ₂. Then
One interesting thing to note here is that every element that isn't the identity has order 2:
(0, 1) + (0, 1) = (0, 1 + 1) = (0, 0);
(1, 0) + (1, 0) = (0, 0);
(1, 1) + (1, 1) = (0, 0).
Contrast this with ℤ₄, where 1 + 1 = 2 ≠ 0. Therefore we can note that
since 1 has order 4 in ℤ₄.1 The other definition we need from last time is the canonical projection map.
Definition: Let G₁, G₂ be groups and G₁ × G₂ be the cartesian product. The canonical projection maps π₁ : G₁ × G₂ → G₁ and π₂ : G₁ × G₂ → G₂ are defined by π₁(a, b) = a and π₂(a, b) = b. Note that the canonical projection maps are surjections – π₁ "covers" G₁, and π₂ "covers" G₂.
Let's do some examples. What group is ℤ₄ × ℤ₆ /⟨(0, 1)⟩ isomorphic to? Recall that
⟨(0, 1)⟩ is the subgroup generated by (0, 1), that is, it is the subgroup
We want to know what ℤ₄ × ℤ₆/H is isomorphic to. The most obvious way to do this is by computing the cosets directly. They are
H itself;
1 + H = {(1, 0), (1, 1), ..., (1, 5)};
2 + H = {(2, 0), (2, 1), ..., (2, 5)};
3 + H = {(3, 0), (3, 1), ..., (3, 5)}.
We could do the addition out and check all possible pairs to see that this group of cosets is isomorphic to ℤ₄. (Each coset really just acts like whatever we add to H − this is our ability to choose representatives of the cosets.) Possible to do, but kind of tedious. Certainly not something we can do if our group is much larger, or even infinite.
The easier way to do this is to consider the projection map π₁ : ℤ₄ × ℤ₆ → ℤ₄ defined by
Then we have
So, by the first isomorphism theorem, and recalling that π₁ covers ℤ₄, we have
So much easier right? Rather than going through all the work of manually computing cosets, we can just use the first isomorphism theorem to do all the heavy lifting for us! This is especially useful if we would have to compute an infinite number of cosets, which we'll look at in the next example.
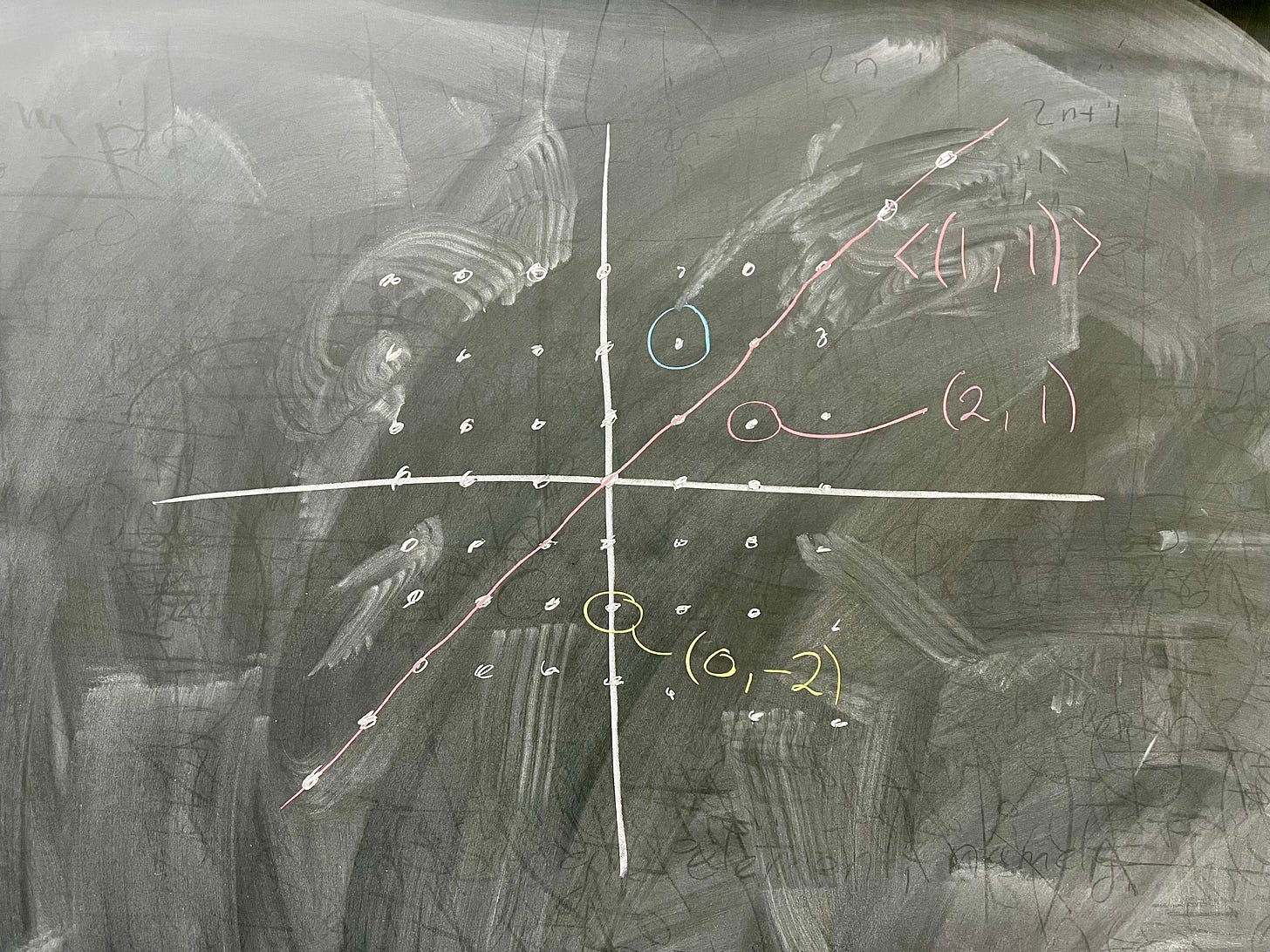
What is the factor group ℤ × ℤ/⟨(1, 1)⟩ isomorphic to? Well, first, let's think about what ℤ × ℤ looks like. This is the set of ordered pairs of integers, that is,
I specify ordered because (2, 1) is not the same as (1, 2).
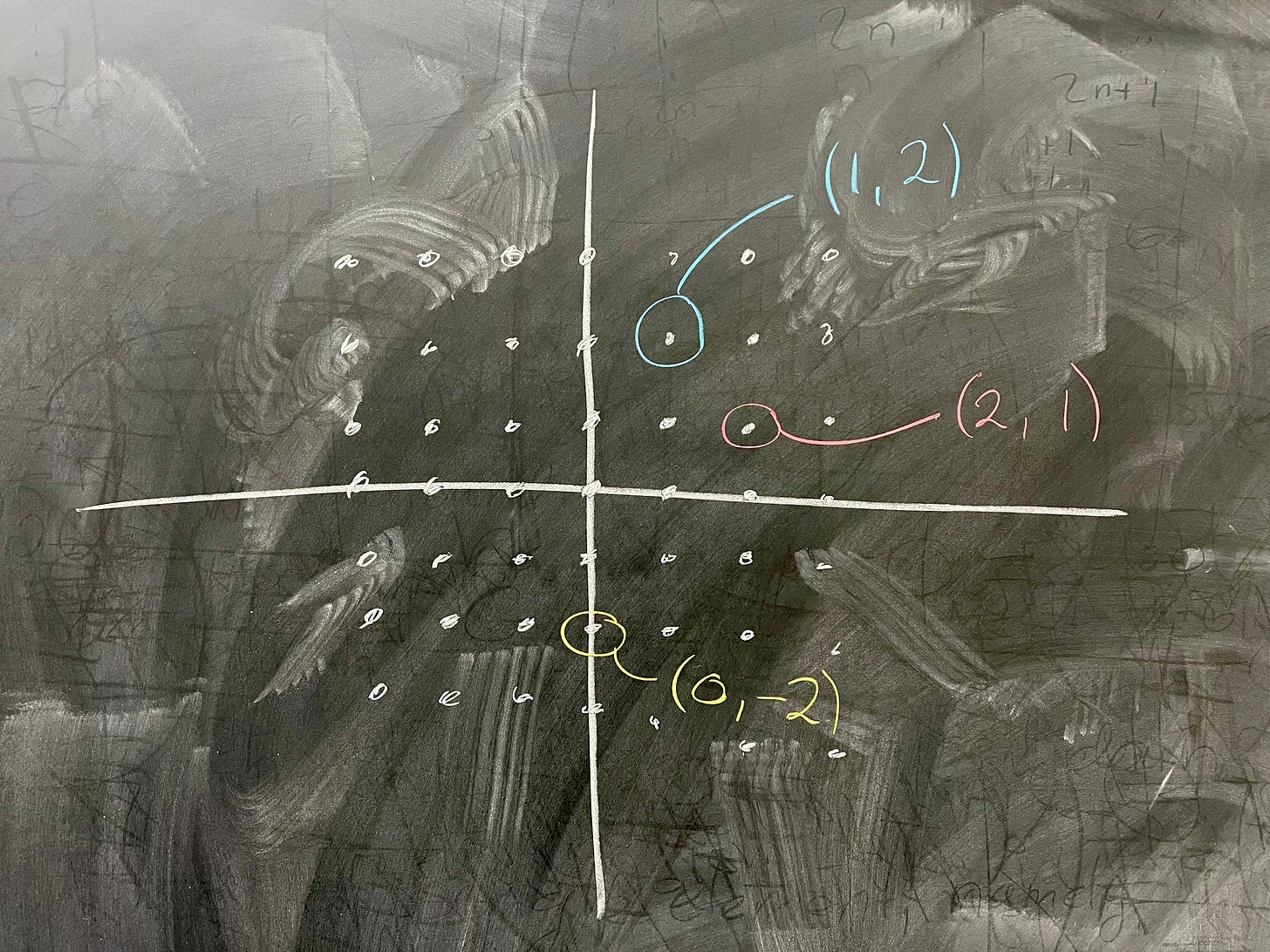
The best picture to have of this group is this grid of integer points in the plane. What does ⟨(1, 1)⟩ look like in this picture? Well, it's all points of the form n(1, 1) where n ∈ ℤ. This is of course the same as the points (n, n), so our picture looks like this:
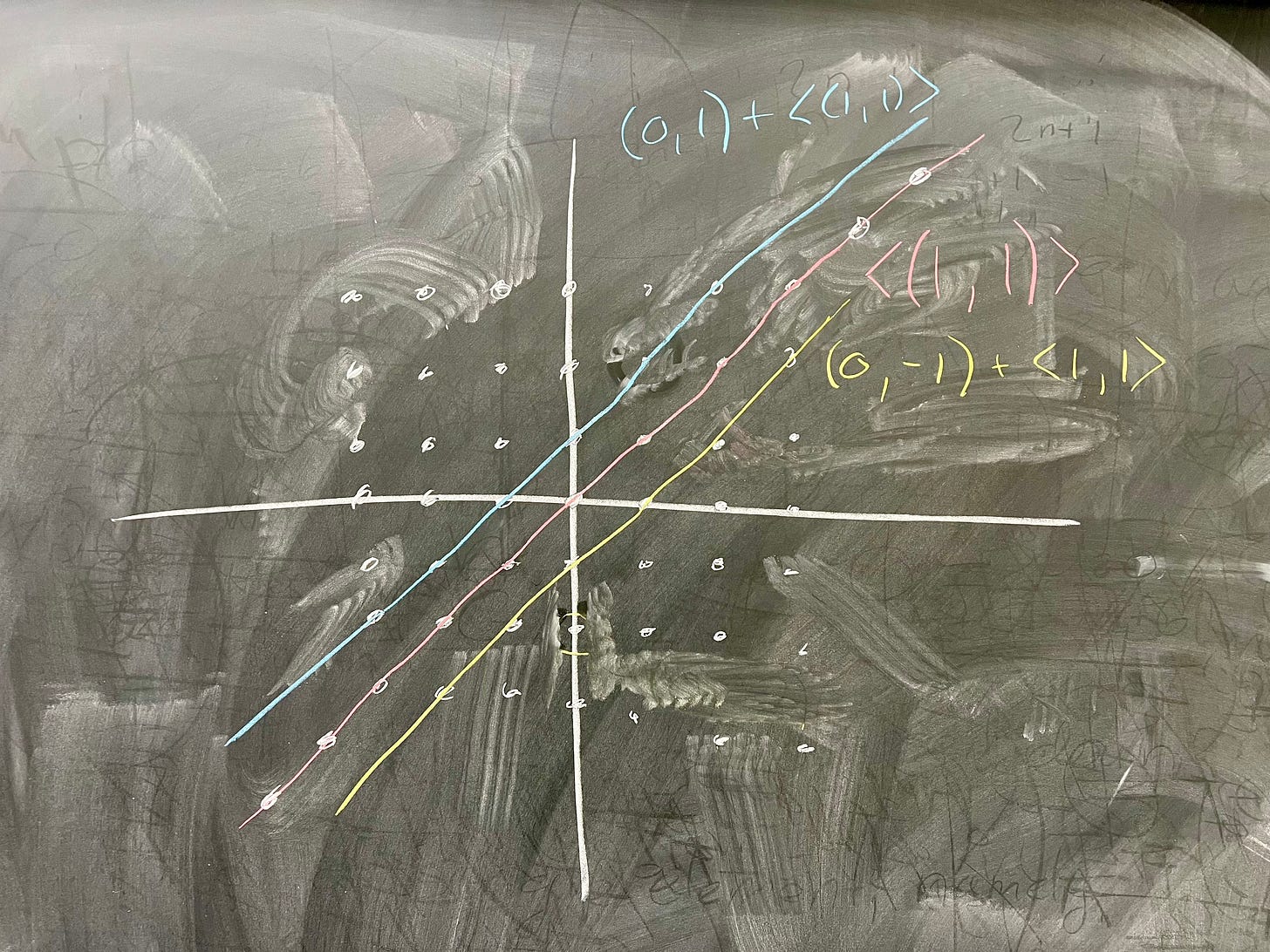
Remember that by considering the group ℤ × ℤ/⟨(1, 1)⟩, what we're doing is saying "alright, what happens if we say all elements in ⟨(1, 1)⟩ act like the identity?" In other words, our identity is no longer just the point (0, 0), but it is any point on the line we drew. So, what are the new elements of the group? Well, let's pick some new point, say (0, 1). Our coset is
So, this new coset, this new element of our group, is our line from before but shifted upwards by 1. Similarly, a point like (1, 0) gives us the coset
If we plot these two cosets, they look exactly like our original line, but shifted up one and down one, respectively:
So intuitively, this group should be isomorphic to ℤ, right? Our identity element is the line x = y, and each new element (coset) of our factor group is that line but shifted up or down by some element of ℤ. Generally speaking, it's good to try and get an intuition for what the group should be isomorphic to before trying to find a homomorphism that gives us our desired result.
Let’s see if we can prove our working hypothesis here. We'll define our homomorphism ϕ : ℤ × ℤ → ℤ given by
The reason you might think to do this is because the way we saw that this should be ℤ is by noting that really, we're tracking the "height" of the line – and how far our coset is above the line ⟨(1, 1)⟩ is given by this factor. We see that ϕ is a homomorphism, since
Now we do the usual thing and compute the kernel. We want all pairs (m, n) such that ϕ(m, n) = 0. But this is precisely the condition that m = n, so our kernel is
Further, the image of ϕ is obviously all of ℤ, since ϕ(0, n) = n for any n. So, by the first isomorphism theorem, we indeed have
Summary
Today we learned the most important concept for understanding the structure of groups, that is, factor groups. These are integral to the study of groups in large part because of the main result we learned today, the first isomorphism theorem. Next time, we'll wrap up our introduction to group theory series (exciting!) by talking about simple groups, and doing a quick overview of one of the most impressive mathematical accomplishments of the 20th century: the classification of finite simple groups.
Exercises
Let H be a subgroup of G, and let G be an abelian group. Show that G/H is abelian.
Let G be a group, and a ∈ G. Recall that ⟨a⟩ is defined as the subgroup {aⁿ | n ∈ ℤ}. Determine whether the following factor groups make sense; if they do, compute their order. Remember that order = size = number of elements in the group. So for example, the order of the group ℤ/4ℤ is 4, since it has four elements.
ℤ/7ℤ.
ℤ₁₆/⟨4⟩.
D₈/⟨s⟩.
D₈/⟨r⟩.
What is ℤ × ℤ/⟨(2, 2)⟩ isomorphic to?
Solutions to Previous Exercises
Go back to the proof that the kernel of a homomorphism is normal, and show that assuming a and b are in the same right coset of ker(ϕ) implies that they are in the same left coset.
Assume that a and b are in the same right coset of ker(ϕ); that is, assume
Then we have b = ka for some k in ker(ϕ), and multiplying on the right by a⁻¹ gives ba⁻¹ ∈ ker(ϕ). For ba⁻¹ to be in the kernel, it must get sent to the identity by ϕ, that is,
Because ϕ is a homomorphism, we can move the inverse outside of the parentheses, and then multiply by it on the right, to get
Since these are equal, we also know that
This means ab⁻¹ is in the kernel of ϕ, which means
as desired.
Find a homomorphism ϕ : ℤ₆ → ℤ₃ with kernel H = {0, 3}.
Define ϕ as follows:
We see that the only values of ϕ which get sent to 0 are 0 and 3; thus our kernel is H. Now, we show that ϕ is a homomorphism. There are two cases:2
m + n < 3; note that if m or n is ≥ 3, our addition +₃ allows us to subtract off 3 as needed.
\(\phi(m +_6 n) = m + n = \phi(m) +_3 \phi(n)\)3 ≤ m + n < 6;
\(\phi(m +_6 n) = m + (n - 3) = \phi(m) + \phi(n) - 3 = \phi(m) +_3 \phi(n)\)
Thus ϕ(m + n) = ϕ(m) + ϕ(n), so ϕ is a homomorphism with the desired kernel.
Find an isomorphism ϕ : ℤ/nℤ → ℤₙ, where ℤ/nℤ is the set of cosets of nℤ in ℤ.
Let G₁ and G₂ be groups. Define the cartesian product G₁ × G₂ to be the set of pairs (g₁, g₂), where g₁ ∈ G₁ and g₂ ∈ G₂. Then we can define a group operation on G₁ × G₂ by
That is, we're doing the group operation "coordinate−wise". Show that G₁ × G₂ is indeed a group under this operation. (An example of this cartesian product would be ℤ₂ × ℤ₂: it would have elements (0, 0), (0, 1), (1, 0), and (1, 1).)
Closure: Let (g₁, g₂) and (h₁, h₂) be elements of G₁ × G₂. We want to show
(g₁, g₂) • (h₁, h₂) is also in G₁ × G₂. By our definition we have
\((g_1, g_2) \cdot (h_1, h_2) = (g_1 h_1, g_2 h_2)\)Since G₁ and G₂ are groups, we know that g₁h₁ is in G₁ and g₂h₂ is in G₂. Thus, our operation gives us another element of G₁ × G₂, so it is closed.
Associativity: By a very similar argument, the associativity of G₁ × G₂ follows naturally from the fact that G₁ and G₂ are themselves associative:
\(\begin{align*} \left((g_1, g_2)(h_1, h_2)\right)(j_1, j_2) &= (g_1h_1, g_2h_2)(j_1, j_2) \\ &= ((g_1h_1)j_1, (g_2h_2)j_2) \\ &= (g_1(h_1j_1), g_2(h_2j_2)) \\ &= (g_1, g_2)\left((h_1, h_2)(j_1, j_2)\right). \end{align*}\)Identity: The identity element in G₁ × G₂ is (e₁, e₂), since
\((g_1, g_2)(e_1, e_2) = (g_1e_1, g_2e_2) = (g_1, g_2)\)Inverses: Let (g₁, g₂) be some element of G₁ × G₂. Then it’s inverse (g₁, g₂)⁻¹ is given by (g₁⁻¹, g₂⁻¹):
\((g_1, g_2)(g_1^{-1}, g_2^{-1}) = (g_1 g_1^{-1}, g_2 g_2^{-1}) = (e_1, e_2).\)
Note that we never had to specify what groups G₁ and G₂ are! They could be any groups whatsoever; all we used to prove that G₁ × G₂ is a group is the group structure of G₁ and G₂.
Let G₁, G₂ be groups. Let π₁ : G₁ × G₂ → G₁ be defined by π₁(a, b) = a, and let π₂ : G₁ × G₂ be defined by π₂(a, b) = b. Show that π₁, π₂ are homomorphisms. (These are called the canonical projection maps, because we're "projecting" our larger group G₁ × G₂ onto G₁ or G₂.)
Let (g₁, g₂) and (h₁, h₂) be elements of G₁ × G₂. For π₁ we have
Similarly, for π₂ we have
Thus π₁ and π₂ are homomorphisms.
What is the kernel of π₁, and what is the kernel of π₂?
Recall that the kernel of a homomorphism is the collection of elements that gets sent to the identity. For π₁ we have
Of course, π₁(g₁, g₂) = e₁ precisely when g₁ = e₁. So our kernel is
Likewise, we see that
If you don’t see why, try to construct an isomorphism between ℤ₂ × ℤ₂ and ℤ₄. What goes wrong when you try to decide what to send to 1?
At various points through this exercise, I am inserting +₃ and +₆ as seems helpful, to recall that the additions are strictly speaking, not the same. Adding 3 in ℤ₆ will give you a different number, e.g., 2 +₆ 3 = 5 in ℤ₆, but in ℤ₃, adding three always gives you the same number, e.g., 2 +₃ 3 = 2 +₃ 0 = 2 in ℤ₃. That’s why we’re allowed to cancel things in the way we are for this exercise.