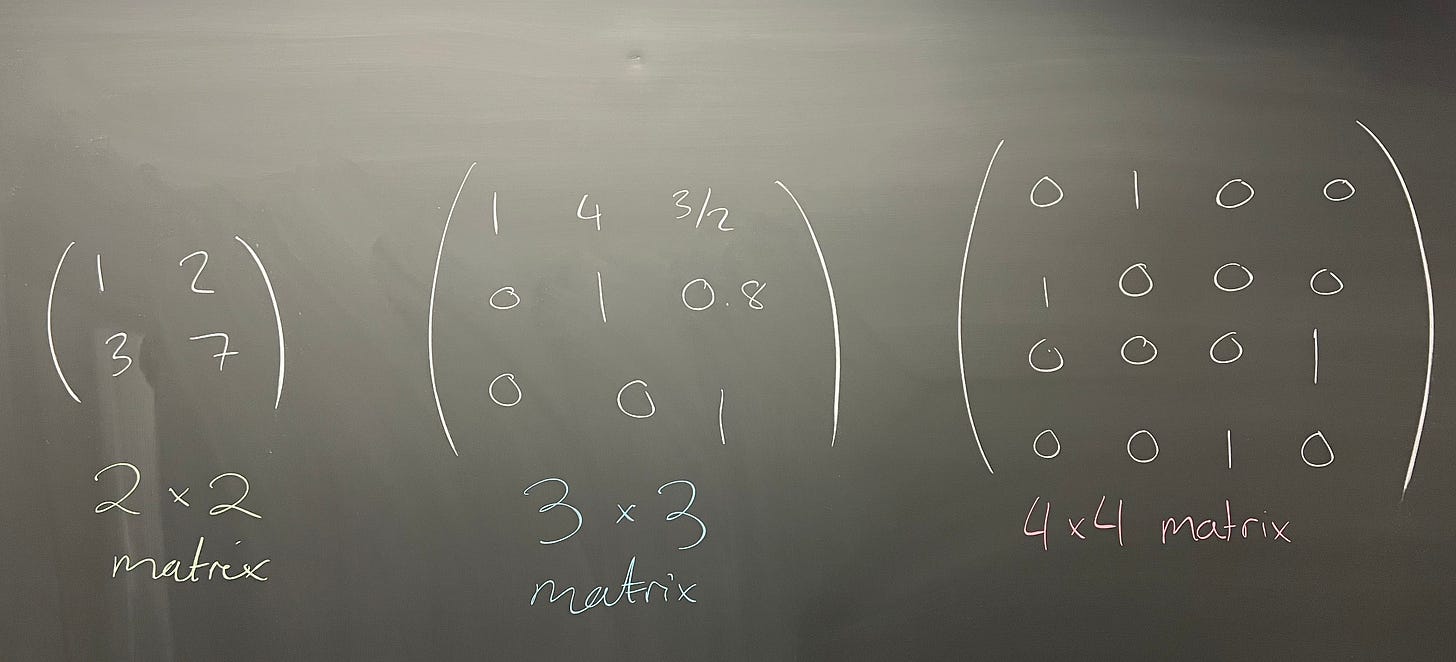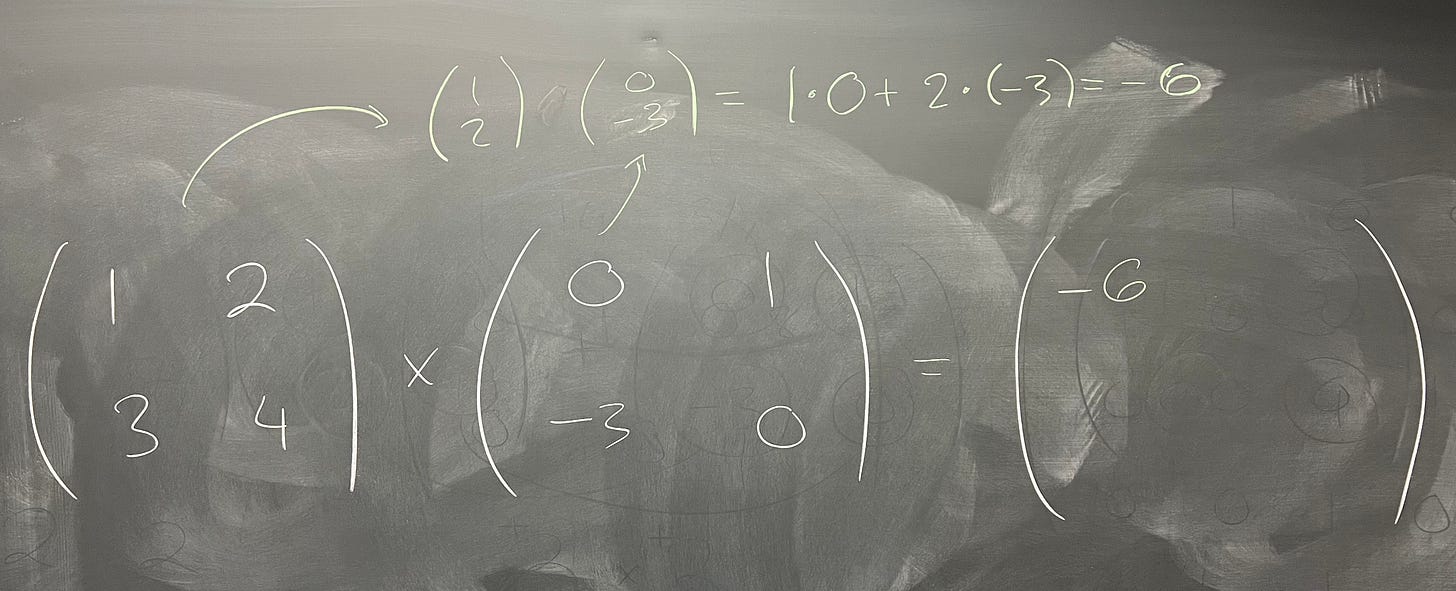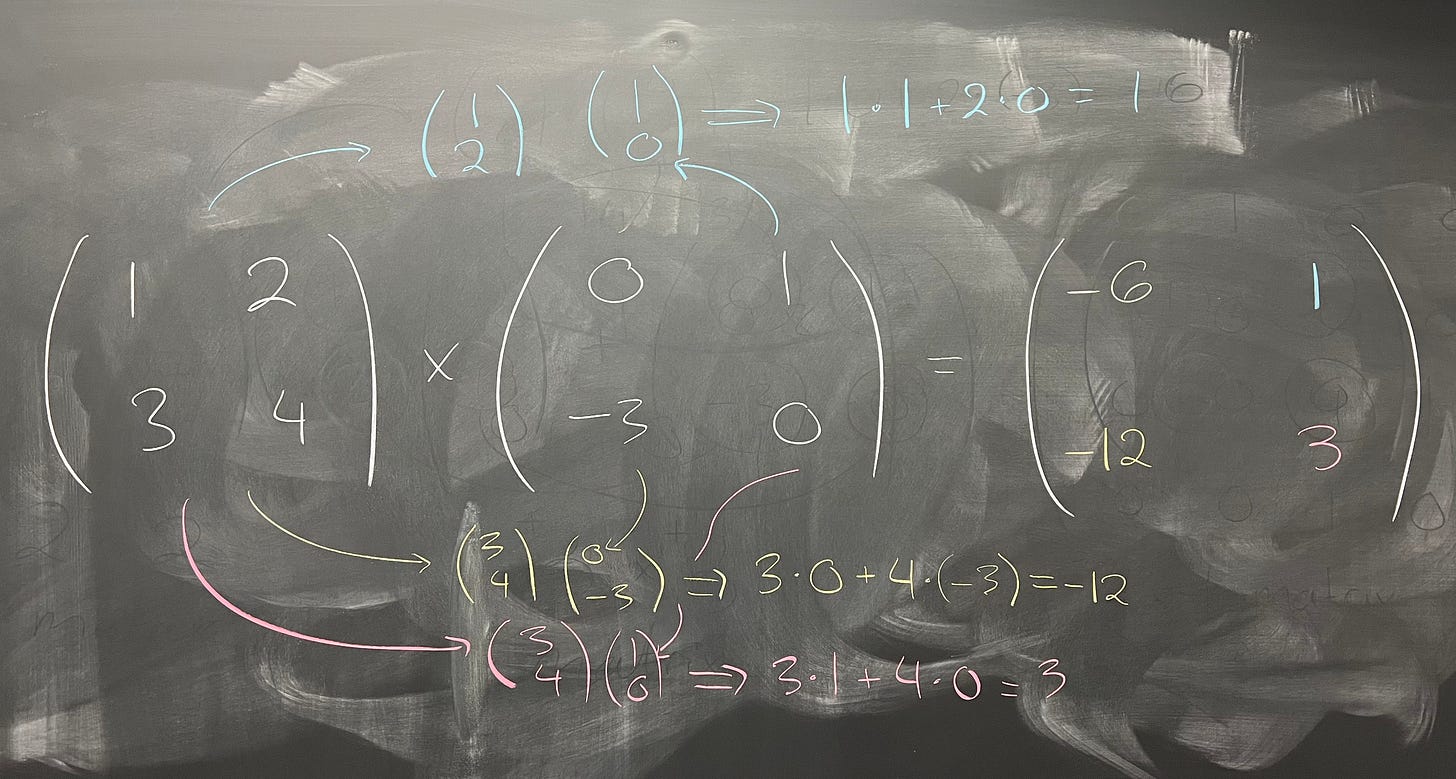Introduction to Ring Theory I

If you liked it, you should've put a ring on it.

We've finally reached the end of the Introduction to Group Theory series, and now get to turn our attention to Rings and Fields. These, like groups, are a kind of algebraic structure. And, once again, they are things that, though you don't know it, you are familiar with. However, Rings and Fields have more structure than groups. In some sense, groups are the "least structured" sort of algebraic object that are really nice, useful things to study.¹ Today we'll start by defining a ring in its most general form, and then look at some examples of rings. Next time, we’ll define an analogue of group homomorphisms, which we call – to the utter amazement and horror of everyone, the crowd gasps – ring homomorphisms.

---

What is a ring?

Informally, rings are sets on which we can define addition and multiplication in the "usual" sense.

So, examples of rings with which you are familiar are

• The integers, ℤ: of course, we can add and multiply any two integers and we will get another integer;

• The rational numbers ℚ, as well as the real numbers ℝ and the complex numbers ℂ.

The rationals are just all the fractions; if I add or multiply two fractions I get another fraction. The real numbers are all the decimal numbers; all the fractions are in ℝ, but so are numbers like √2, π, things like that. If you haven't seen the complex numbers before, don't worry about it, we'll get there in due time. (Actually, all these examples are also fields, not just rings; we'll get to fields a bit later in the series. Fields are the "nicest" possible algebraic structure.)

You might have wondered if our groups ℤ/nℤ could have multiplication on them as well, and indeed, you can. For example, ℤ/5ℤ is a perfectly well−defined ring, because multiplication works exactly the same way addition does; you just subtract off multiples of 5 until you're in the right range. For example, 2 times 3 is 6, but we subtract off 5 to get 1. So in ℤ/5ℤ, 2 × 3 = 1. Similarly, 4 × 3 = 2, etc. Those are some examples of rings, so now let's see the formal definition.

Definition: A ring (R, +, ⋅) is a set R together with two binary operations, + and ⋅, which we call addition and multiplication, defined on R so that the following axioms are satisfied:

• (R, +) is an abelian group;

• Multiplication is associative, that is,

  \(a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c\)

  for any a, b, c ∈ R, and there is a unit element 1 ∈ R such that

  \(a ⋅ 1 = 1 ⋅ a = a\)

  for all a;

• For all a, b, c ∈ R, the left and right distributivity laws hold; that is,

  \(a ⋅(b + c) = a ⋅ b + a ⋅ c\)

  and

  \((a + b) ⋅ c = a ⋅ c + b ⋅ c.\)

When dealing with rings, we will always denote the additive identity as 0. That is, 0 will always be the element such that 0 + x = x. Similarly, we say that 1 is the multiplicative identity.²

There's a fourth property, which much like groups, we don't require, but we do want to give a name to. If a⋅b = b⋅a for all a, b, then we say that the ring is commutative.

Notice that all of our examples given above are commutative rings. We'll generally talk about commutative rings during this series, although I will give one important example of a non−commutative ring that will come up again very often later on in the representation theory series. And, one note on notation: it is common to write ab for a⋅b, and I will use this convention liberally. So, the left distributive law could be rewritten as

\(a(b+c) = ab + ac.\)

Let's check and make sure that these laws work for one of our examples. The integers will be our touchstone example for a ring; it turns out almost all the important properties one could want in a ring are found in the integers.

We already saw during the group theory series that (ℤ, +) is an abelian group. We also know, just from our basic experience, that if I take any three numbers, it doesn't matter what order I multiply them in. For example,³

\(2 ⋅ (3 ⋅ 4) = 2 ⋅ 12 = 24,\)

and

\((2 ⋅ 3) ⋅ 4 = 6 ⋅ 4 = 24,\)

so indeed they are equal. Let's also briefly check left distributivity: we have

\(2 ⋅ (3 + 4) = 2 ⋅ (7) = 14,\)

and

\(2 ⋅ 3 + 2 ⋅ 4 = 6 + 8 = 14,\)

so indeed they are the same. It should be clear that this will hold in general, for ℤ. (Unofficial exercise; pick your three favorite integers, and check that right distributivity works on them as well.)

Now we'll take a look at a different example. Recall our subgroups nℤ of ℤ. They are defined by all the integer multiples of n, namely,

\(nℤ = \{..., −2n, −n, 0, n, 2n, ...\}.\)

Is this a ring? Clearly, it satisfies the first criterion, which is that (nℤ, +) is an abelian group. Multiplication is of course associative, since multiplication in ℤ is also associative. Likewise, distributivity holds here because it holds in ℤ. It is also closed under multiplication. To see this, pick two elements of nℤ, call them nr, ns. Then we indeed have

\((nr)(ns) = nrns = nnrs = n(nrs) ∈ nℤ.\)

So this is nearly a ring, as we've defined it; however, it does not contain the multiplicative identity, 1 (unless you’ve chosen n = 1). This is an important example of something called an ideal, which we'll define in a few weeks.

Now, for some more notational clarifications. Let R be any ring. We will always denote the identity element of the additive group, namely (R, +), with 0. For any element a ∈ R, we will let its additive inverse (that is, its inverse in the group (R, +)), with −a.

Frequently, we will have cause to refer to the sum

\(a + a + a + ⋯ + a,\)

where there are n copies of a. We shall let this be denoted by n × a, and for this we will always use the cross.⁴ This is important, because n may not be in the ring at all.

For example, consider the set 2ℤ of even integers. If we pretend for a moment that 2ℤ is a ring, I still cannot write 3(2), because 3 is not in the "ring" of even integers. However, I can consider 3 × 2, because as we've defined it, this is just 2 + 2 + 2 = 6. Make sense?

If n < 0, then we define n × a = (−a) + (−a) + ⋯ + (−a), where there are |n| copies of −a. Finally, we define 0 × a = 0, where 0 on the left is the integer 0, and 0 on the right is the zero in the ring. Remember, with the cross, this means "add a to itself 0 times". If this is going to mean anything at all, it must mean, well, zero!

Okay, now that we have all that notation out of the way, it's time for our first theorem.

Theorem: Let R be a ring with additive identity 0. Then, for any elements a, b ∈ R, we have:

1. 0a = a0 = 0 (remember that this is not the same as 0 × a);

2. a(−b) = (−a)b = −ab;

3. (−a)(−b) = ab.

Proof: For the first property, note that, using our distributivity axioms for a ring,

\(a0 + a0 = a(0 + 0) = a0 = 0 + a0.\)

Of course, since (R, +) is a group, we can cancel one a0 on each side (by adding −a0, if you like) to get a0 = 0. Similarly,

\(0a + 0a = (0 + 0)a = 0a = 0 + 0a, \)

so again we see 0a = 0.

For the second property, remember that −ab is, by definition, the element that when added to ab, gives us 0. So, we want to show that a(−b) + ab = 0; if this holds, then a(−b) is also the inverse of ab, which means −ab = a(−b). By the left distributive law,

\(a(−b) + ab = a(−b + b) = a0 = 0,\)

where the last equality is true because of our just−proved property one. Likewise, applying right distributivity gives

\((−a)b + ab = (−a + a)b = 0b = 0.\)

So, indeed, (−a)b = a(−b) = −ab. Finally, by repeated application of our second property, we have

\((−a)(−b) = −(a(−b)) = −(−ab) = ab.\)

This completes the proof. ☐

---

An Important Non−commutative example

What follows is a foundational example that we will use a lot when we approach Linear Algebra. These are rings of something called matrices. If you haven't seen a matrix before, that's fine! I'm going to breeze through some of the relevant details now, but fear not, we will return to this later. If this doesn't really make sense to you yet, that's okay.

Essentially, a matrix is just a grid of numbers. I'll focus on the 2 × 2 case today, but in general we could have 3 × 3 matrices, 4 × 4 matrices, n × n matrices:

I'll denote the set of 2x2 matrices with real entries—that is, each individual number in the matrix is some real number—by M₂(ℝ). Adding two matrices together works in exactly the way you would guess. We look at each spot on the matrix, and add them together. An example of this is

\(\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix} + \begin{pmatrix}0 & 1 \\ −3 & 0\end{pmatrix} = \begin{pmatrix}1 & 3 \\ 0 & 4\end{pmatrix}.\)

This addition is commutative; it can be shown that we have all the usual group structure we want, so we're well on our way to showing that M₂(ℝ) has a nice ring structure. What's our multiplication?

The way matrix multiplication is defined is not what you would hope. We don't get to just multiply "by slot" in the same way we defined addition. Instead, we have to do something weird: take the top row of the left matrix and the left column of the right matrix. Then, take each entry on the left, and multiply it by its "corresponding" entry on the right. Then, add those two numbers together. That will be the first (top left) entry of our new matrix.

The top right entry of the new matrix will be the same exact process, except now we use the right column of the right matrix. The bottom entries, similarly, will be the same process, except with the bottom row of the left matrix.

So, taking our two entries from before, we would have

\(\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}\begin{pmatrix}0 & 1 \\ −3 & 0\end{pmatrix} = \begin{pmatrix}−6 & 1 \\ −12 & 3\end{pmatrix}.\)

I promise you, there is a good reason for defining multiplication this way. We will get to it later, when I cover linear algebra, but until then you'll just have to trust me. Alternatively, you can also just go watch 3blue1brown's excellent series, Essence of Linear Algebra, on YouTube. (Indeed, you should watch this series regardless.)

Note that this multiplication is NOT commutative! If we take the same two matrices as before but switch them, we get

\(\begin{pmatrix}0 & 1 \\ −3 & 0\end{pmatrix}\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix} = \begin{pmatrix} 3 & 4 \\ −3 & −6\end{pmatrix}.\)

Since we get two different matrices when we switch the order, this means that, while M₂(ℝ) is a ring, it is not a commutative ring.

---

Summary

Today we covered a new kind of algebraic structure, called a ring. We walked through what a ring is, and gave some basic examples. Next time, we’ll consider ideas that are directly analogous to what we looked at for groups, namely, ring homomorphisms.

Exercises

1. In this exercise, we'll show that M₂(ℝ) is a ring. In what follows, I will let

   \(D = \begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}.\)

   1. Show that M₂(ℝ) is an abelian group under addition. That is, you must show that adding any two 2×2 matrices together gets you another 2×2 matrix; that the addition is associative; that there is an identity element (what is it?), and that every matrix has an inverse. What is the additive inverse of D?

   2. What is the multiplicative identity for M₂(ℝ)?

   3. Show that matrix multiplication distributes over addition from the left. That is, for any matrices A, B, C ∈ M₂(ℝ), show that

      \(A(B + C) = AB + AC.\)

      (If you want a bonus, show that right distribution also works.)

2. Take the matrix D and multiply it on the left and the right (that is, if A is our new matrix, compute both AD and DA) by each of the following matrices:

   1. \(A = \begin{pmatrix} 0 & 0 \\ 0 & 0\end{pmatrix}.\)

   2. \(B = \begin{pmatrix} 1 & 2 \\ 2 & 1\end{pmatrix}\)

   3. \(I = \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}.\)

1. This is mostly true. There are occasions where we care about things like monoids, which are groups, except without inverses, and a couple other things like this, but those are pretty rare situations.

2. Some authors require that all rings have the element 1; other authors do not. I am requiring that all rings have a multiplicative identity here.

3. Here I am using the dot, because writing “23” for “2 times 3” is a horrible idea. But in general, unless I’m dealing with digits like this, I probably won’t use the dot.

4. This is my own convention for the series, and not anything standard as far as I’m aware. The reason I’m doing this is just to avoid confusion for you, the reader; in general, it’s often written just like normal multiplication in the ring, and it’s left to context to determine what is meant.