The Splitting Piles Problem

Or, why mathematics is just as much art as science...

In 1988, over 250 of the brightest mathematical teenagers in the world gathered in Canberra, Australia to compete in Earth's most prestigious, and difficult, mathematics competition: the International Mathematical Olympiad. Nearly fifty countries sent teams of 6 teenagers, who were not allowed to be enrolled in a university, to compete. This grueling exam is given over two days, with 4.5 hours for each day, and only three(!) problems given per day. All problems were entirely proof-based; no points for getting the "correct" answer unless you correctly justify why that is the correct answer. Each student is scored from 0 to 7 on each problem, making the maximal score a 42. Surely these kids were all so talented that they all got 7s on every problem, right? Wrong!

It was at this IMO that a legend was born: the Legend of Question Six. I'll briefly state it to give you, dear reader, some mathematical street cred:

1988 IMO Problem 6: Let a and b be positive integers such that ab + 1 divides a² + b². Show that

\(\frac{a^2 + b^2}{ab + 1}\)

is the square of an integer.

That's it! That is question six. This is the problem that was so hard, it stumped all but eleven of the students there! (Albeit, in addition to the 11 students who earned 7s, one student each scored a 4, 5, or 6.)

Part of what makes this problem so legendary is that the committee in charge of determining the IMO problems took 4.5 hours – three times the amount the students would get – to try and solve this problem, and could not. They put it on the test anyway.

I'm not going to talk about this problem, though. For one, Numberphile has already covered it far better than I can – go watch this video, if you like. No, I want to talk about something that may confound any non-mathematical person if they happened upon the IMO standings list from that year: a little thing in that image, on the right at the top, that says "special prize". The natural question is, of course, "What could cause someone to get a special prize at the IMO?" Indeed, this is an excellent question; this special prize was given out because of how elegant, how beautiful his proof was for the legendary Problem 6.

Most people are completely confounded when I tell them I find math "beautiful" or "elegant", or that I view mathematics as an art as much as a science. And yet I do find math beautiful and elegant, and believe it is an art and a science, in roughly equal parts. Today, I want to walk through an easier, but still interesting, problem, and show you the differences in two possible solutions to this problem. I'll first show you the different solutions, and afterwards, talk about where I see beauty in each of them.

---

The problem

The setup for the problem is as follows:

Imagine you have N coins in a single pile, and your score starts at 0. Whenever you split a pile, say of size k, into two piles, of size m and k - m, you add m × (k - m) to your score. You play this game until every pile is of size one, that is, until every pile has a single coin. What is the maximum possible score you can get?

An example of splitting a pile into two piles – in this case, we have k = 7 and m = 3. That is, we split a pile of 7 into a pile of 3 and a pile of 4.

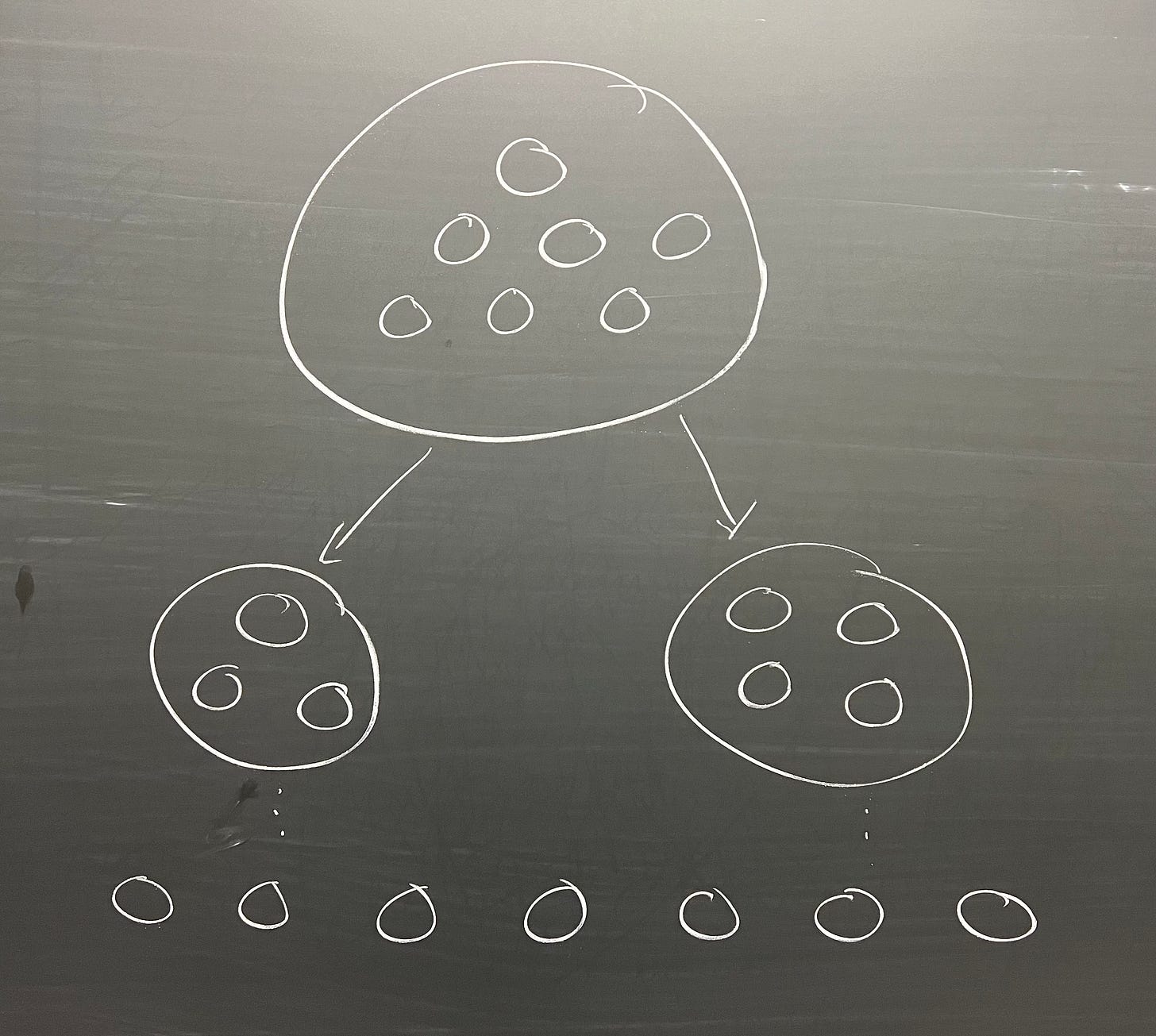
The picture above would score 12 points, because we split a pile of seven into a pile of 3 and a pile of 4, and 3 × 4 = 12. The reason this problem is tricky is that it isn't just asking for one specific value of N. If the game were specified to start with, say, 7 coins, it would take a little while to compute, but eventually we could churn through the calculations and find whatever the answer is. Our problem is harder though, because we have to find the maximum score for every possible value of N. We don't just want to know the maximum for 7 coins, or 5 coins, or 21,347 coins, but all games of all possible size. What this really means is we have to find a formula for the maximum score, based on N.

One thing you learn to do on a problem like this, before you really start trying to "solve" the problem, is to do some really simple cases. What's the simplest case, here? Well, it's when N = 1, that is, when we have one coin. Since every pile has one coin, the game is over, and our score is 0. Not particularly interesting, but good to note nonetheless. What about when N = 2? Well, then we only have one possible move, namely to split the pile of two into two piles of one:

Since we made a real move, we get to add to our score. Yay! We split our pile into two piles of 1, so we get to add 1 × 1 = 1 to our score. So, the maximum score for N = 2 is 1.

What about when N = 3? Once again, we only have a single possible move – split the pile of three into a pile of one and a pile of two:

We need notation to describe this more efficiently; rather than saying "split the pile of three into a pile of one and a pile of two," I'm just going to write

\(3 \mapsto (1, 2).\)

(Note that there's no order to this – what I wrote is the same as 3 ↦ (2, 1).) I'm also going to write S(N) to be the maximum score for N coins. Since we did 3 ↦ (1, 2), we get to add 1 × 2 = 2 to our score. The 1-pile is done, and the 2-pile we already saw adds 1 to our score. Thus, the max score for N = 3 is 3; that is, S(3) = 3.

At N = 4, we finally have a choice! We can either start with 4 ↦ (1, 3) or 4 ↦ (2, 2).

If we start with 4 ↦ (1, 3), then we add 1 × 3 = 3 to our score. The 1 is done, and the 3 adds another 3 to our score, so we get a total score of 3 + 3 = 6. If instead we did 4 ↦ (2, 2), we add 2 × 2 = 4 to our score, and each 2 adds another one, so again we get a score of 6. This means that our choice actually didn't change the final score − thus S(4) = 6. Bit strange that the choice didn't matter, huh? Let's do one more.

For N = 5, our two choices are 5 ↦ (1, 4) or 5 ↦ (2, 3):

If 5 ↦ (1, 4) is our choice, then we add 4 to our score, and then note that the 4−pile adds 6 to our score. So this choice gives us 10. Likewise, if we do 5 ↦ (2, 3), we add 6 to our score, the 2−pile gives us 1, and the 3−pile gives us 3, so the total is again 10. Thus our choices are irrelevant once again, and the score is S(5) = 10. Weird, right?

It's at this point (or perhaps after checking N = 6, which you may do on your own) that, if you're a mathy person who does this sort of thing for fun, that these numbers we're getting for the scores are the triangle numbers. What are the triangle numbers, you ask? Well, they're the numbers you get from summing consecutive integers starting at 1; that is, the first few triangle numbers are:

• 1

• 1 + 2

• 1 + 2 + 3

• 1 + 2 + 3 + 4

• etc.

The reason they're called triangle numbers is because if you do this out with a picture, they look like, well...triangles:

(Indeed, for N = 6 we find S(6) = 15.) In particular, if the 1st triangle number is 1, then the nth triangle number is given by

\(\frac{n(n+1)}{2}.\)

Check this for some small values of n to convince yourself it works. Our scores here are slightly offset, however; our conjecture is that we have

\(S(N) = \frac{N(N-1)}{2}.\)

We have to offset by one, since S(2) = 1, not S(1) = 1. So, with this eminently reasonable conjecture in place, how might we go about actually proving this is true?

---

Solution 1: Induction

The first solution we're going to talk about uses an incredibly important and ubiquitous tool in the mathematician's toolbag: induction. Essentially, the way induction works is you show that your claim is true for some sort of "base case" – think of this as like a starting point – and then you show that, if it's true at some step k, then it must be true at step k+1.

This means that it's true for all possible k, because you've shown that it's true at your starting point, and you've shown that if it's true at one step, then it's true at the next step.

Let's sketch this method out with something very simple. In fact, what we're going to do is go back and prove that the nth triangle number is, indeed, n(n+1)/2, by induction.

Proving the triangular numbers formula

Base case: Our base case should clearly be n = 1. We can see, based on our pictures, that our 1st triangle number should be 1. Plugging in n = 1 to our formula, we get

\(\frac{1(1+1)}{2} = \frac{1 \times 2}{2} = 1.\)

That's it for the base case; let's now prove that our inductive step.

Inductive step: First, we assume that our formula works for some n = k. This means that we have the kth triangle number being

\(1 + 2 + \cdots + k = \frac{k(k+1)}{2}.\)

Recall that the nth triangle number is defined by

\(1 + 2 + \cdots + n,\)

that is, adding the first n numbers. So, the (k+1)th¹ triangle number is

\(1 + 2 + \cdots + k + (k+1).\)

We have a formula for 1 + 2 + ... + k, so lets plug that in. We get

\(\frac{k(k+1)}{2} + k + 1.\)

You might recall that one thing we like to do in math is to write everything over a common denominator. Multiplying by 2 and then dividing by 2 doesn't change our value, so we can rewrite k+1 as 2(k + 1)/2. Plugging this in gives us

\(\frac{k(k+1)}{2} + \frac{2(k+1)}{2}.\)

We can, of course, combine these fractions, which gives us

\(\frac{k^2 + 3k + 2}{2} = \frac{(k+1)(k+2)}{2}.\)

This is exactly what we wanted to show, because if we plug in n = k+1 to our formula we get

\(\frac{(k+1)(k+1+1)}{2} = \frac{(k+1)(k+2)}{2}.\)

So we're done! We've shown that our formula is true in the base case, and then we've shown that the formula being true at any point implies it's also true at the next point. So, our formula being true at 1 implies it's true at 2, and being true at 2 implies it's true at 3, all the way down.

Back to the main problem

Now that we've seen how induction works, we can use it on our problem. We've shown for some small values of N (in particular, N = 1, 2, 3, 4, 5) that the formula

\(S(N) = \frac{N(N-1)}{2}\)

is true. This can serve as our base case. Now, let's assume that the formula holds from 1 up to some N = k. This is our inductive step. We want to show that this implies it must be true at N = k+1. Well, how do we do this? We have k+1 coins, and we know that our formula works from 1 all the way up to k, which means any move we do will split the coins into two piles where we can use our formula:²

Therefore, let's assume that our first move is to split into a pile of m and whatever is left over – in this case, it's k + 1 - m. (If you add these together, you find that they add back up to k + 1, which is good. Wouldn't want coins mysteriously showing up or disappearing into the aether.) Then our new score will be the max we can get from m coins, plus the max we can get from k + 1 - m coins, plus the score we get from our move - that is, m(k + 1 - m). Writing all this out we see

\(S(k+1) = S(m) + S(k+1-m) + m(k+1-m).\)

Since m ≤ k + 1 and k + 1 - m ≤ k + 1, we can apply our formula to both of them:

\(S(k+1) = \frac{m(m-1)}{2} + \frac{(k+1-m)(k - m)}{2} + m(k+1-m).\)

If you multiply all this out and put it all over a common denominator, you get

\(\frac{m^2 - m + k^2 - mk + k - m - mk + m^2 + 2mk + 2m - 2m^2}{2}.\)

Notice that we’re going to get a lot of cancellation here. For example, we have m² at the front, a second copy of m² in the middle, but then a -2m² at the end – they all cancel. If we cancel out everything we can, we are left with

\(\frac{k^2 + k}{2} = \frac{k(k+1)}{2}.\)

Indeed, if you plug in N = k + 1 to our formula we get the same thing, so we're done! We've shown that our maximum score, S(N), is equal to N(N-1)/2 for all N.

---

Solution 2: Graph Theory

We're going to start by doing something a little weird. We're going to set up a "graph" – but this is not the usual sense of graph that you might've seen in algebra class, with an x axis and a y axis. No, this is a different kind of graph. We're going to have some points, which we call "vertices", and some lines connecting them, which we call "edges":

In particular, we're going to let each coin be represented by a vertex, and we will draw an edge between two coins if they are in the same pile. So, our starting positions for N = 3 and N = 5 would look like this:

In general, these graphs will have N vertices, and everything will be connected to everything else. These are called the complete graphs on N vertices. Here’s the complete graphs for 9, 10, 11, and 12 vertices:

These would correspond to our starting positions with 9, 10, 11, or 12 coins. Now, let's count the number of edges. If I label the vertices 1, 2, ..., N (we'll continue using the example N = 5 in our pictures), then we can label all of our edges as pairs of vertices. The edge going from 1 to 2 can be (1, 2), the edge from 4 to 5 can be (4, 5), etc. Note that (4, 5) is the same as the edge (5, 4); I'll always list them in the order (smaller, larger) since they're equivalent.

Note that I made a labeling mistake – the top label should say (2, 5), not (2, 4).³ The way I'm going to count them is by starting with all the edges of the form (1, ...):

As we can see, there's the edge (1, 2), then (1, 3), all the way up to (1, n). There would be n edges, then, except the edge (1, 1) doesn't exist, so we have n-1 edges. Next, we count the edges of the form (2, ...). Importantly, we don't count (2, 1)! We've already counted (2, 1), in the form (1, 2), so we can skip it. Similarly, there's no (2, 2), so our first edge is (2, 3). We again go all the way up until (2, n), which gives us n-2 numbers. The pattern continues, giving us n-3, then n-4, all the way until the edge (n-1, n). How many edges do we have? Well, we have

\((n-1) + (n-2) + \cdots + 3 + 2 + 1.\)

We've seen this before! This is just the (n-1)th triangle number, so we can rewrite that as N(N-1)/2 as before. This is interesting – there are exactly as many edges to start with as our final score.

What does our graph look like once we reach the final state? Well, every coin is in its own pile, so we get a completely disconnected graph:

So, we started with N(N-1)/2 edges, and the end state of the game has zero edges. If we could show that every point we get corresponds to an edge being lost, then we're done! But this is obviously true: if we start with a pile of m+n coins that we split into piles of size m and n, then we lose mn edges:

(Here we've used m = 3 and n = 4 for our example.) Essentially, we've "cut" the graph into two pieces - everything on one side of the cut keeps its connections, but any edge that crosses the cut gets deleted. Each vertex in the m-pile will lose n edges – one edge for each vertex in the n-pile – and there are m vertices in the m-pile, so we lose mn edges.

This is exactly the score we add when we make this move, so we're done! The maximum score is always N(N-1)/2, because we've shown that every point we earn corresponds to losing an edge in our graph, and we start with N(N-1)/2 edges and end with 0 edges.

---

So...where's the beauty?

Before I tell you about the beauty and where I see it, I would love to hear about what you think the more beautiful solution was, and why you think that.

Did you go comment? I'm serious.

Some of the more mathematically inclined-or-experienced readers may expect me to say that the second solution is the only beautiful one, and the first one is ugly. But actually, I think they're both very beautiful solutions – the beauty comes from different places.

Yes, it is true, the second solution is far more elegant, to me, than the first one. The second solution reduces the problem down to something where you can really see the why behind the answer. The second solution is like a blacksmith's hole punch. It opens up the heart of the problem. Simple, beautiful, precise. Why is the answer what it is? Well, because there's always going to be N(N-1)/2 edges in a complete N-graph. The solution to the answer is the same as the number of edges in that graph, so we're done! Induction, by contrast, does not really give us any such insight in the same, visceral way. It's easy to do the induction without getting a grasp of why the induction works.

This doesn't mean induction is less beautiful though. Induction's beauty comes from its raw power. If the second solution is like a hole punch, then induction is like a hammer. Incredibly versatile, useful in more places than you can count; just as you'd never catch a blacksmith without a hammer, so would you never catch a math professor not knowing what induction is. As beautiful as the second solution is, you can't use it in other places. It's specialized – just like the hole punch. A hole punch is excellent at what it does, but it isn't good at much else. A hammer, in contrast, is one of the fundamental tools of the trade. Induction has been used to prove many things: a few examples, off the top of my head, are

• The formula for triangle numbers (which we saw today);

• The formula for the sums of squares, cubes, and in general, summing

  \(1^n + 2^n + 3^n + \cdots + k^n\)

  for any integer n;

• Fermat's Little Theorem: if p is a prime and a is an integer, then

  \(a^p \equiv a \mod p\)

• Mihăilescu's Theorem: (Also know as Catalan's Conjecture) The only solution to the equation

  \(x^a - y^b = 1\)

  where a, b, x, y are integers, with a, b > 1, x, y > 0, a ≠ b and x ≠ y, is x = b = 3, a = y = 2. Or, in English, there are no two perfect powers separated by 1, except for 2³ = 8 and 3² = 9. (Induction comes up in some specialized cases in the proof.)

• Of course, the legendary question 6, which we discussed earlier.

If you're usually a non-mathy person, I would love to hear your thoughts. Did you find this at all convincing? Or are you left as confused as before as to why people such as myself describe math as beautiful? Please let me know your thoughts down below in the comments.

1. (k+1)st? (k+1)nd?

2. Technically, we’re using strong induction here, because we’re assuming that it holds for all 1, 2, 3, …, k, rather than just true at k. But in practice, these are basically the same, so it’s not worth distinguishing for this article.

3. Mathematicians are notoriously bad at numbers.