Introduction to Group Theory II
Ahwt's a ttmpuoreain?
Last time, we saw the definition of a group and covered some basic examples of groups. Today we're going to talk about a pivotal and recurring example, called the Permutation Group, and we'll also prove some foundational facts about groups. Before we get there, though, let's refresh on what a group is.
A group is a pair (G, •), where G is a set whose members we call elements, and • is a closed binary operation on G. Further:
The binary operation • is associative on G: that is, for all a, b, c in G, we have
\(a \cdot (b \cdot c) = (a \cdot b) \cdot c.\)There exists a unique identity element e in G, which satisfies, for all a in G,
\(a \cdot e = e \cdot a = a.\)For every a in G, there exists a unique inverse b in G, commonly denoted a^-1, which satisfies
\(a \cdot a^{-1} = a^{-1} \cdot a = e.\)
We’re using the dot, •, here as a stand-in for any binary operation we happen to be using. All the normal math operations you’re used to are binary operations: addition, subtraction, multiplication, etc. The reason we’re using • in our definition is because the binary operation for a group can be any of those. In fact, it can be something like “composition” as well, which we saw in last week’s article. You might remember from our last installment that one of our examples was a standard clock face. In that example, our set was the numbers
and the operation was addition1. In our triangle example, the set was
and the operation was composition.
One thing you might notice about those sets is that the identity is unique in both of them. That is, there is only one identity element in each set; it is 12 in the former case, e in the latter. You might wonder: is this always true?
Are Identity Elements Unique?
Suppose that we have some group G, such that G has two identity elements. Let's call them e and f. If we can prove that e and f are equal to each other, then we know that G only really has one identity element. Make sure you understand this idea - we're assuming that e and f both refer to identity elements, and if we can show they are equal, then they must refer to the same identity element. That is, there cannot be two "different" identity elements.
Consider the element
On the one hand, we know that e is an identity element, so we must have
On the other hand, we know that f is also an identity element, so we must have
Putting this together, we have
This means that e = f, so we're done! They have to be the same element. Of course, this means that there cannot be groups with three identities, four identities, etc., because we can consider any two of them and apply this argument.
Some people may ask the question "Why is this important?" Well, because it justifies the use of the word unique in our definition of a group:
There exists a unique identity element e in G, which satisfies, for all a in G,
\(a \cdot e = e \cdot a = a.\)
We really don't want to live in a world where we say "the identity," but not be sure if that is well-defined. This raises the question - are inverses unique?
What About Inverses?
The way we attack this problem is very similar to how we attacked it for the identity. Suppose we have a group G that contains an element g which has two inverses: let's call them h and j. As before, we want to show that h and j are equal to each other.
Consider the element
Well, we know that j is an inverse of g, which means g • j = e: this tells us
Note here that associativity is why h • g • j is well-defined to begin with. If we did not have associativity, we would have to specify either h • (g • j) or (h • g) • j, and those may not be the same without associativity. By the same idea as with the identity, h is an inverse of g, so we have
Putting all this together, we have
This means that h and j are actually the same element, which is precisely what we wanted. We care about this result for the same reason we care about the identity - we want to be able to choose any element of a group, and talk about the inverse.
It's worth pausing here for a moment and thinking about the power of what we just proved. The uniqueness of the identity and of inverses is not something we proved for specific groups. It is something that we proved for all groups. Because of these arguments, if you have a group, then identities and inverses are unique.
What's a function?
Before we get to our special example, we have to understand what a bijective function is.
First, what's a function? Well, a function f is a way of taking in elements in one set, called your domain, and assigning them elements in another set, called the co-domain. We write this as follows: if A is our domain, and B is our co-domain, and f is a function from A to B, we write
This should make sense - our function takes in something in A, and spits something out in B. Also, when we want to write “the element that f sends x to,” we write f(x), which is read “f of x”. Importantly, we require that the function cannot assign the same input multiple outputs - in other words, we cannot have
There are two special kinds of function that we're going to care a lot about: injections and surjections.
A function is an injection if every input gets a unique output. One way of saying that is if f(a) = f(b), then a = b. (Make sure you see why those mean the same thing!) The name injection should make sense - we're injecting our domain A into the co-domain B. No element of A gets sent to the same place in B - everything is uniquely identified.
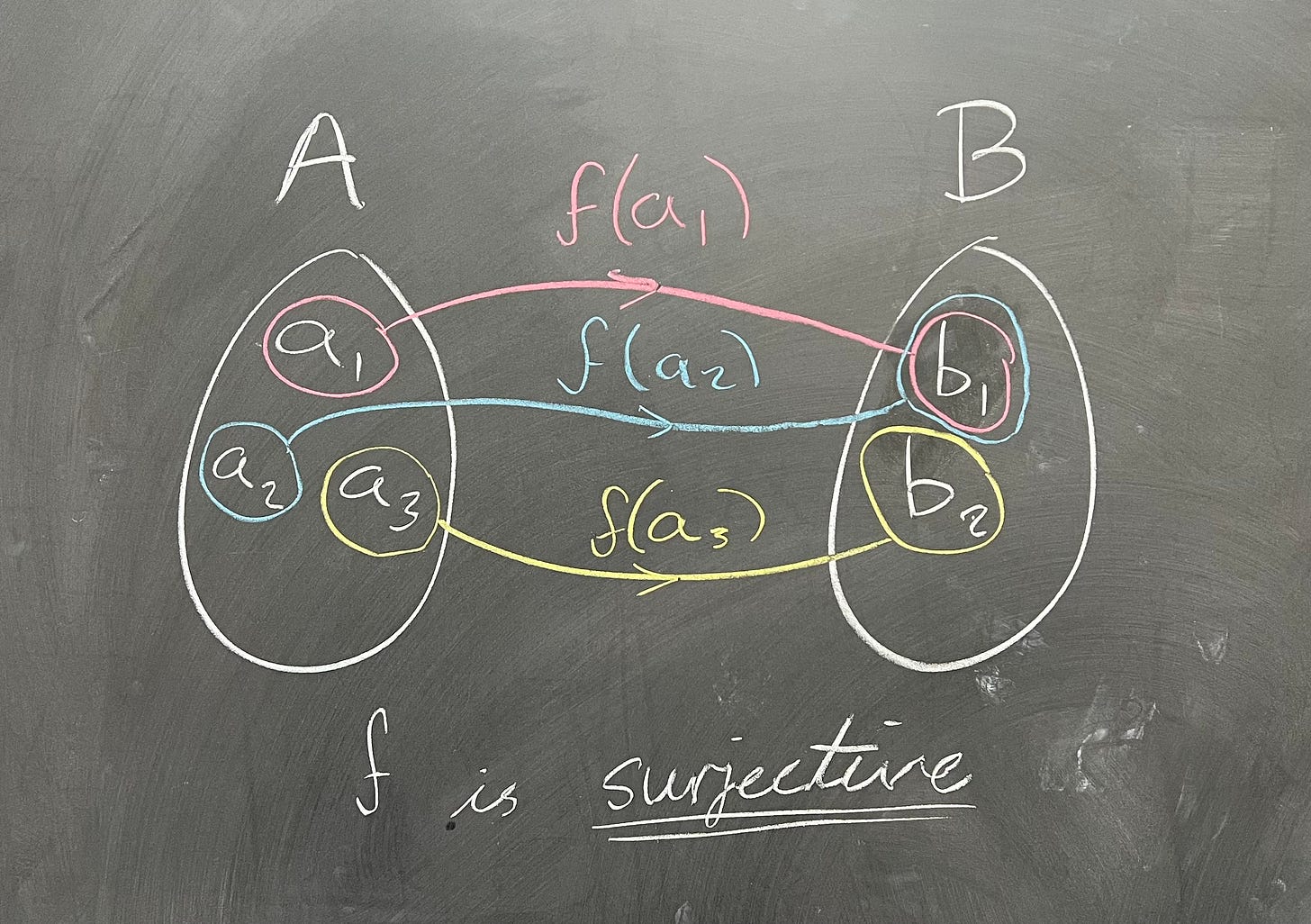
A function is a surjection if every output has a corresponding input (possibly more than one.) Concretely, if we pick some b in our co-domain, then there is at least one a in our domain such that f(a) = b. The name surjection also makes sense, because sur- as a prefix in French means "on top of", and our function f is kind of covering B with A. Every element of B has an associated element of A.
If a function is a surjection and an injection, we call it a bijection. Bijections are also sometimes called one-to-one functions; this is ambiguous, nowadays, because some authors use one-to-one to mean injective only. Intuitively, though, the name one-to-one makes sense: a one-to-one function (bijection) assigns every input with an output, and every output with an input. Everyone is paired up. Bijections are very nice functions, because any bijection automatically has an inverse function: if f is a bijection, we can define the inverse of f, denoted f^-1, by "reversing the direction". That is, if f(a) = b, then f^-1(b) = a. Note that
The Permutation Group
Now we're going to switch gears a little bit and talk about a very important example. As one might guess by the section title, it is called the Permutation Group, and it will continually walk alongside us in our trek towards the distant peaks of representation theory.
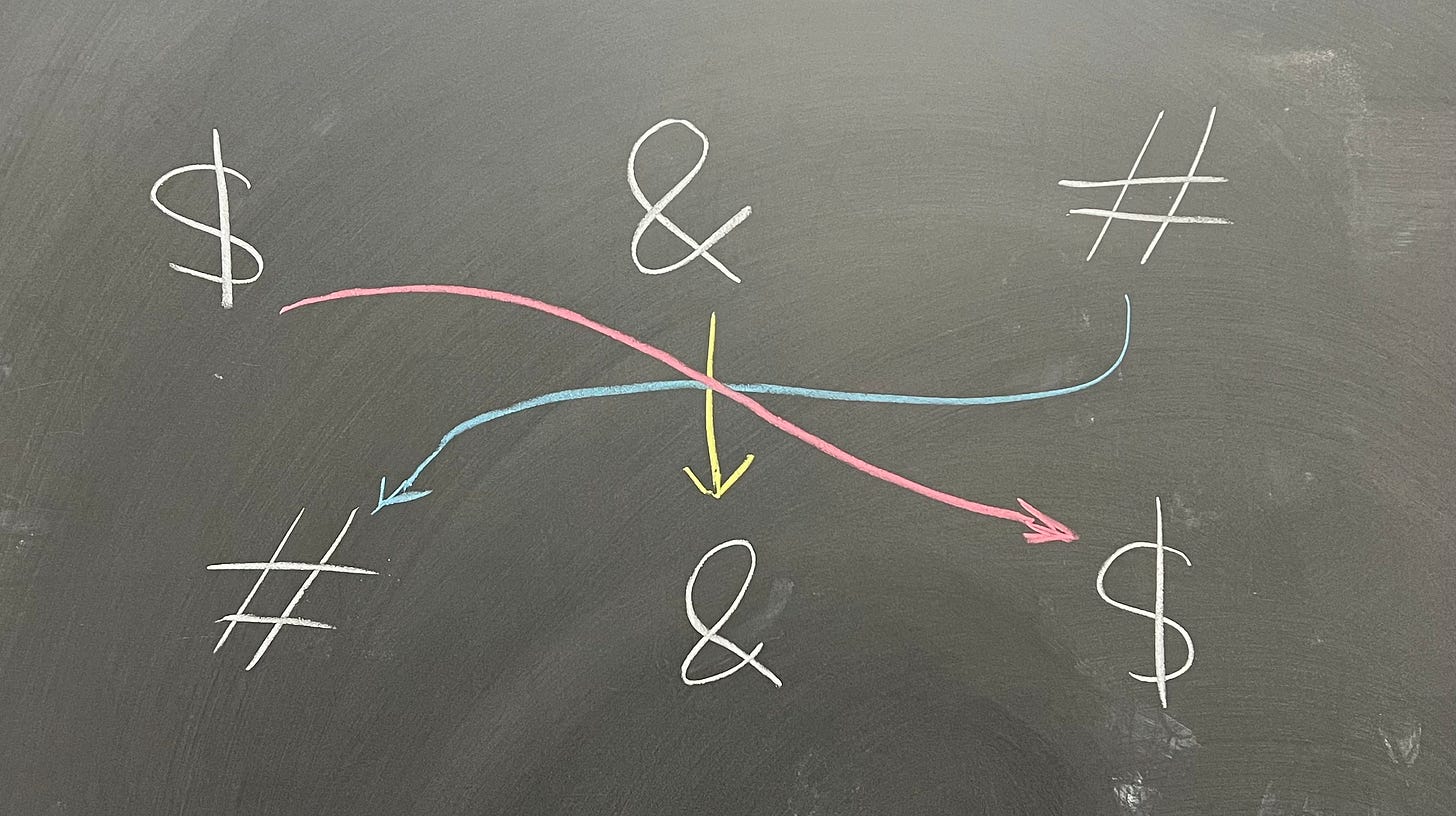
When we're talking about permutations, we're thinking about them in the context of some collection (set) of objects, which are in some order. Informally, a permutation is just switching the ordering around:
In this example, we had $, &, #, and our permutation sent them to #, &, $. Note that & did not move - that's perfectly fine. In fact, as you might guess, a very important permutation is the identity permutation; it does nothing:
Note that both of our examples so far are permutations of three things. Of course, we can consider more than just permutations of three objects - in general, we will consider the permutations of n things, where n is some positive integer.
We really don't care about what the things we're moving around are - they could be red, blue, yellow, or 1, 2, 3. What we care about is what the permutation does to the elements, not the elements themselves. Because of this, we will always use 1, 2, ..., n from here forward.
Now, why did we go through all the trouble of defining functions and injections and surjections? Because, as some of you may have noticed, permutations are bijections! More explicitly, they are bijections from {1, 2, ..., n} to itself; that is, every member of this set gets assigned another member of this set, possibly itself.
Knowing that permutations are bijective functions is a very valuable fact - for example, we know automatically that every permutation has an inverse, since every bijection has an inverse. Since this is an article on group theory, and groups require inverses, this is something we care a lot about.
Let's see if we can flesh out a very simple example. What are all the permutations on the set {1, 2, 3}? Well, we already saw one element, the identity. As before, we'll call it e. Next, there's the permutation that swaps 1 and 2, but leaves 3 fixed:
We need a good way to notate this, so let’s write (1 2) for this permutation. We think of this as saying that 1 gets sent to 2, and then 2 loops back around and gets sent to 1. From this, we see that there are two more swaps we could do, namely
(1 3) and (2 3):
That's all the possible permutations that swap only two elements: what about permutations that shift all three? Let’s start by choosing where to send 1 - say, to where 3 is. We can't send anything else to 3, so we have to send 2 and 3 to 1 and 2, in some order. But we can't send 2 to 2, because then 3 goes to 1, and we just have (1 3). So, 2 goes to 1, and 3 goes to 2. We write this as the cycle (1 3 2) - that is, 1 goes to 3, 3 goes to 2, 2 goes to 1:
Likewise, if we send 1 to 2, then 3 cannot go to 3 and must go to 1, so 2 goes to 3, and we have the cycle (1 2 3).
We have just shown all the permutations of three elements. Now, this is an article on group theory, so a good question is "Is this a group?" (If you've done a class in Bayesian statistics, your answer should probably already be "yes", but that's another story.) We've already seen the identity element, and clearly each permutation has an inverse - intuitively we can just "swap back" to get to the identity. Formally, we see that because permutations are bijective functions, we automatically have inverses. Our binary operation, then, is function composition (which just means do one function/permutation, then do another). Clearly, composing permutations gives you another permutation, so our operation is closed. And finally, it is well-known that function composition is associative2. We call this group of permutations on three elements S_3. And, in general, the group of permutations on n elements will be called S_n.
Summary
Today we covered some very important material. We
Showed that identity elements and inverses are unique; a group cannot have two or more identities, and every element’s inverse is unique;
Defined functions, and discussed what makes a function injective or surjective;
Talked about the permutation group on n elements, which we denote S_n.
As we learn more about groups, it will become clear why the permutation groups are so important. I should also note that, in a format like this, re-reading a sentence or a paragraph should be expected from time to time. We're covering a lot of new ground with each article, so it will often take some time to wrap one's mind around the concepts, and that's okay.
Exercises
Choose any permutation in S_3 - that is, any permutation of three elements - and show that it is an injection and a surjection (and, therefore, a bijection).
Think about the groups D_63 and S_3. Do you see any relation between them? Each group has 6 elements - see if you can find some kind of natural "correspondence" between the two.
(Challenging) How many elements are in S_4? What about S_5, and in general S_n?
Solutions to previous exercises
For each element of D_6, find an inverse for that element.
The inverses of the elements of D_6 are as follows, where (x, y) means x and y are inverses of each other: (e, e), (r, r^2), (s, s), (rs, rs), (r^2 s, r^2 s).
Show that the symmetries of a square, which is called D_8, is a group. You can assume that composition is associative.
Since we are assuming that composition is associative, we just need to show that the symmetries are closed, have an identity, and have inverses.
The set is closed because any two symmetries of the square combine to make another symmetry of the square.
The identity element exists, and just as before it is the "do nothing" element.
Each element has an inverse: (e, e), (r, r^3), (r^2, r^2), and each reflection is its own inverse. (Picking one reflection to be s, we can write the other three as rs, r^2 s, and r^3 s).
Technically, our operation was not truly addition but something called modular addition. There’s a difference here, because true addition would say 8 + 9 = 17, while our modular addition says 8 + 9 = 5. We’ll talk about this difference more in the next couple installments.
Proving that function composition is associative, however important it may be, is a boring and dry endeavor, and would require far more technicality and Sahara-like exposition than this format allows. If you want a visual proof, a nice short video can be found here.
If you don’t know what D_6 is, the first article explains the basics of what a group is, and talks about the group D_6 in some detail.


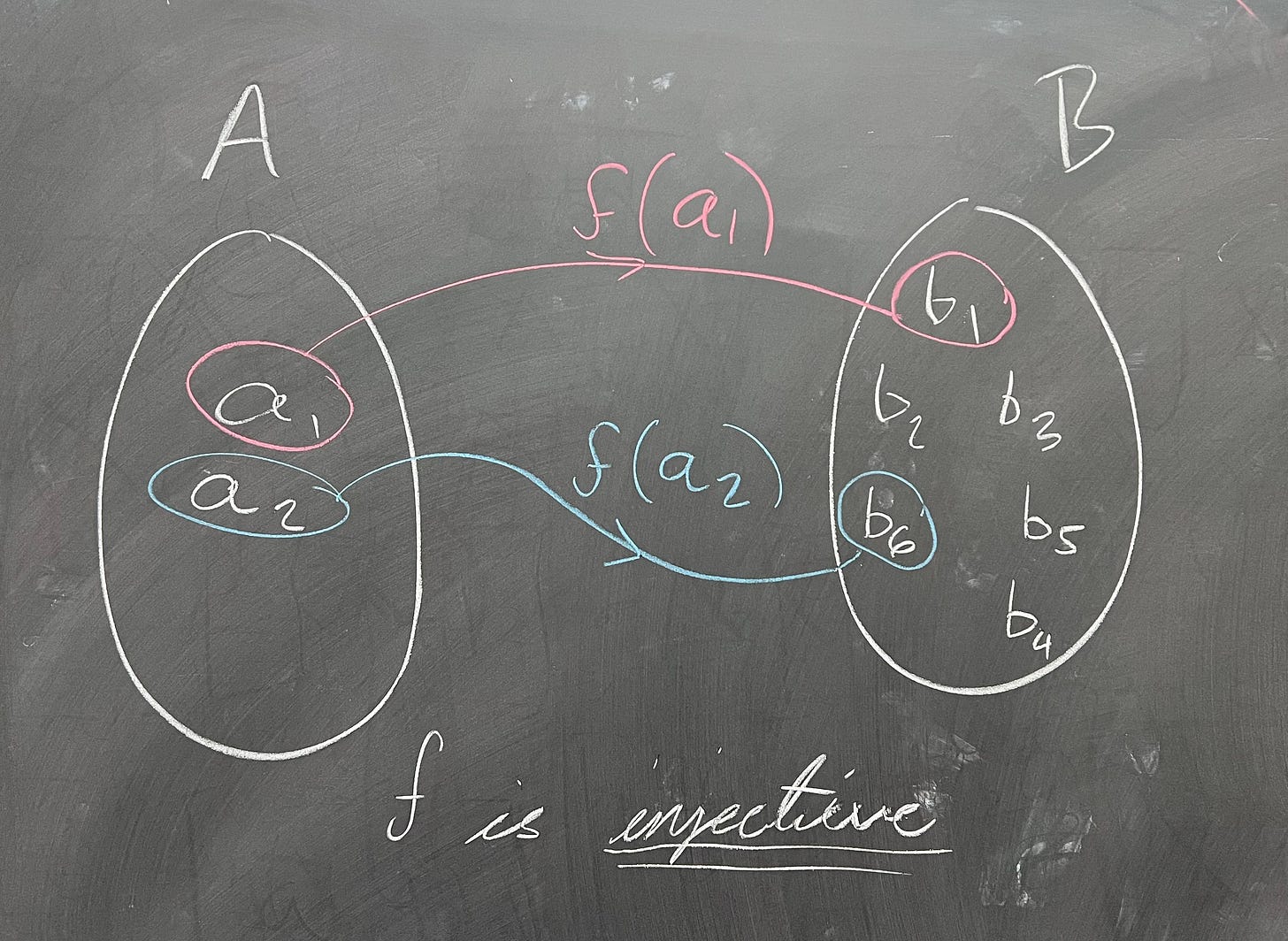
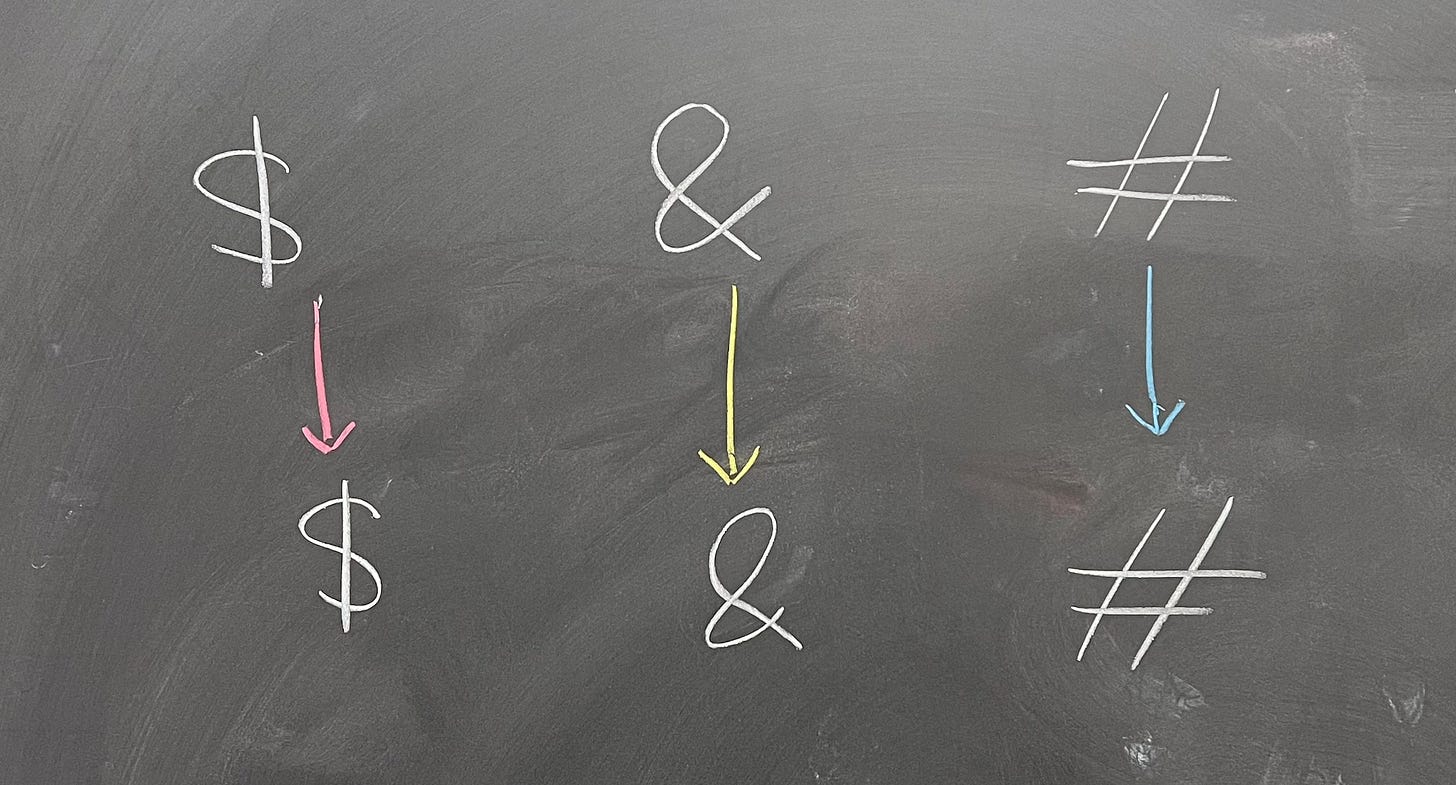
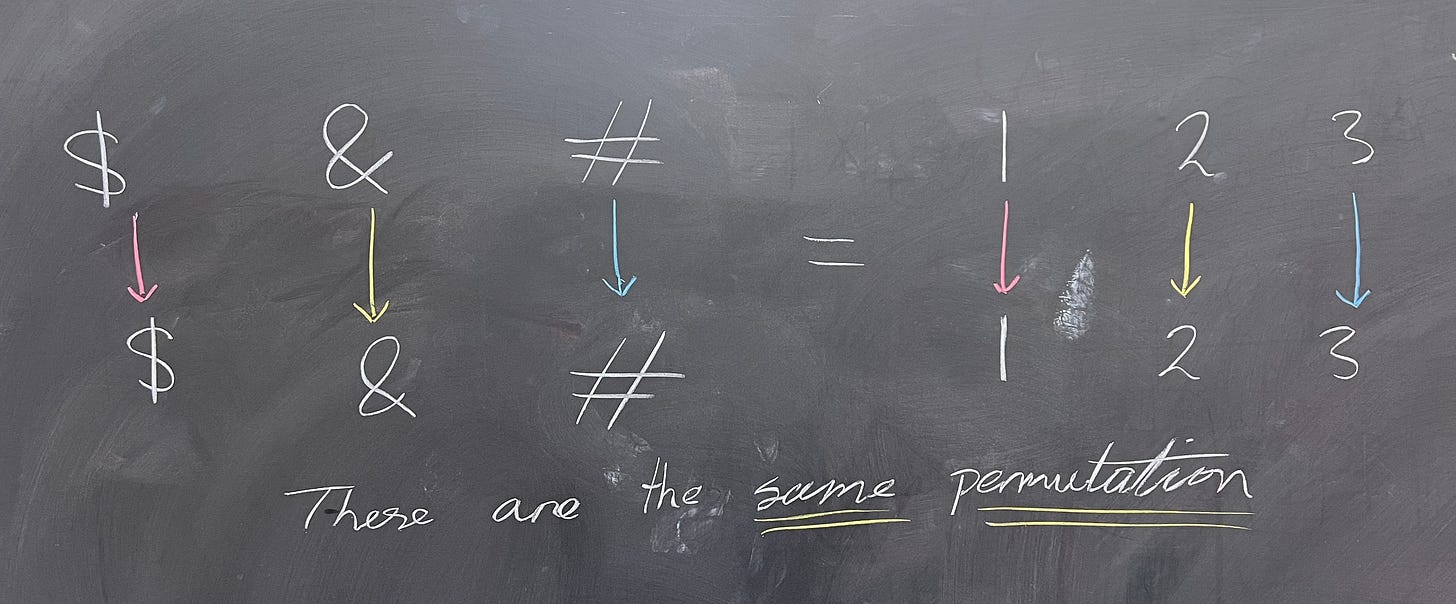
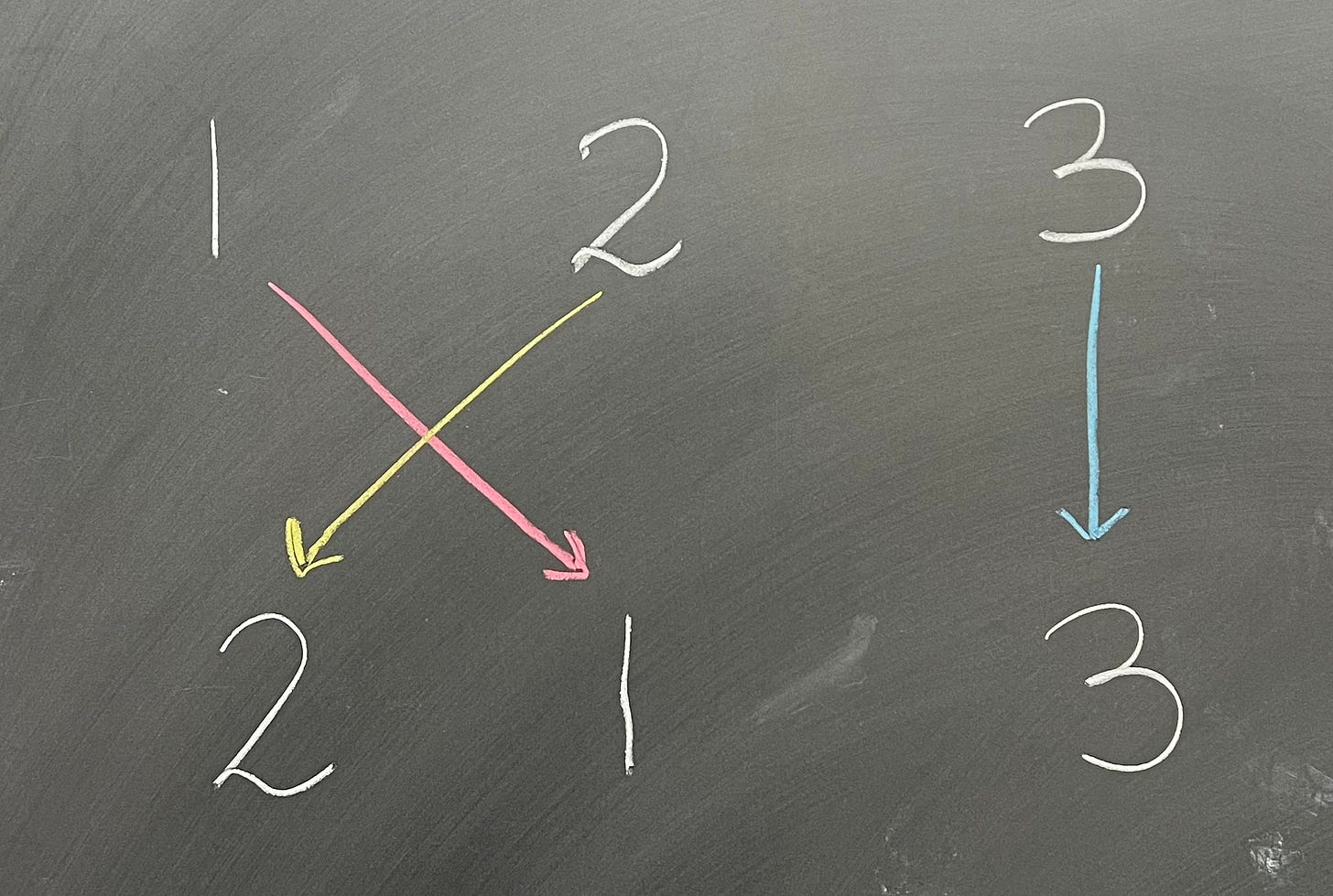
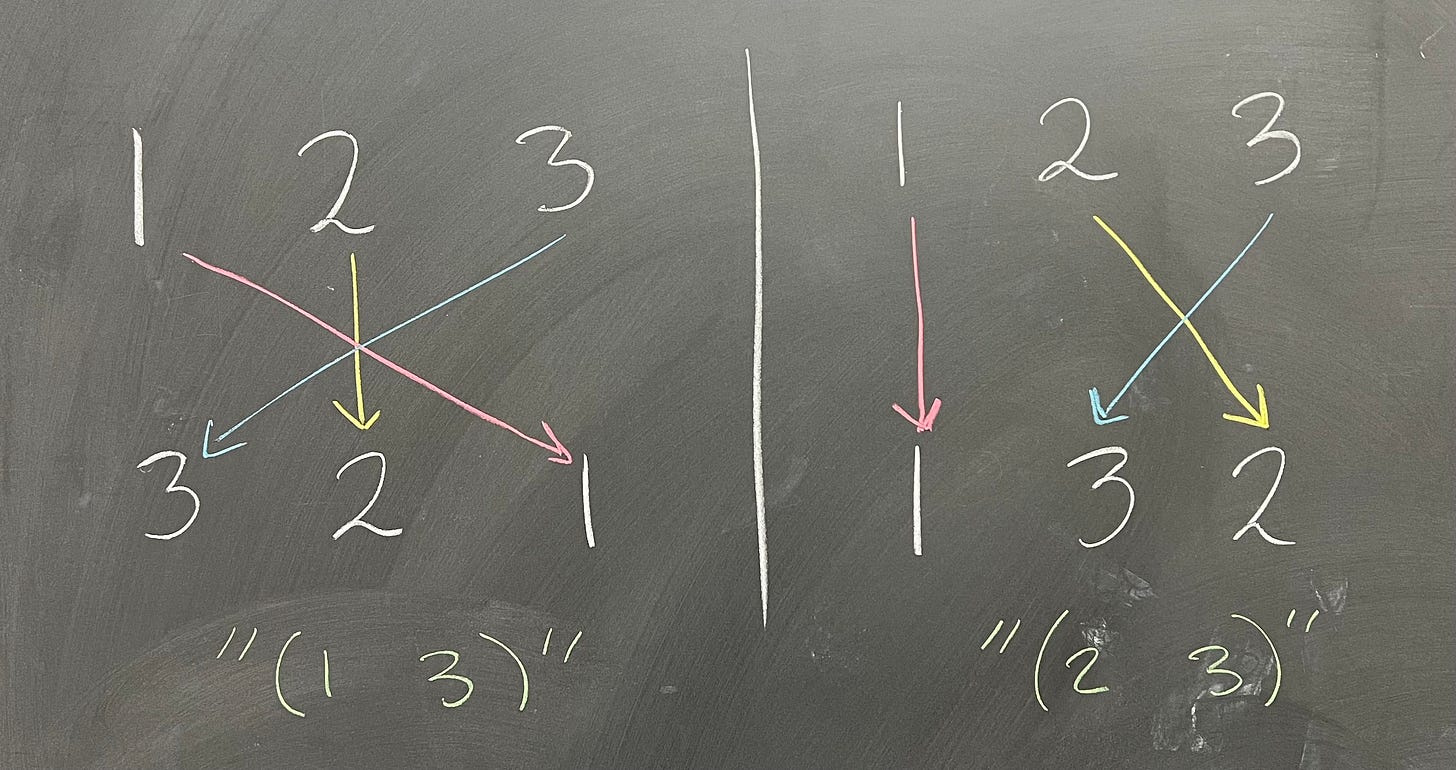
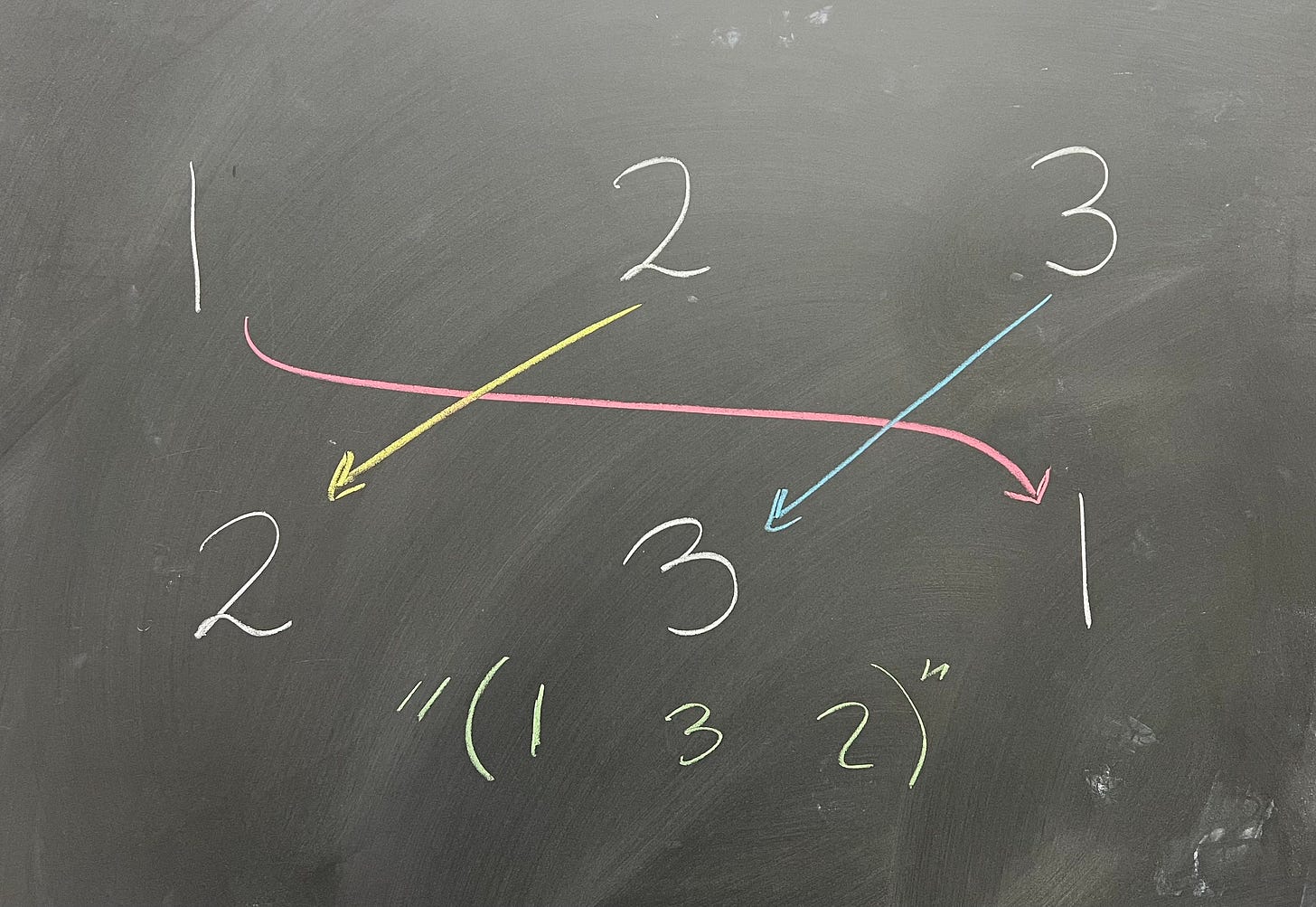
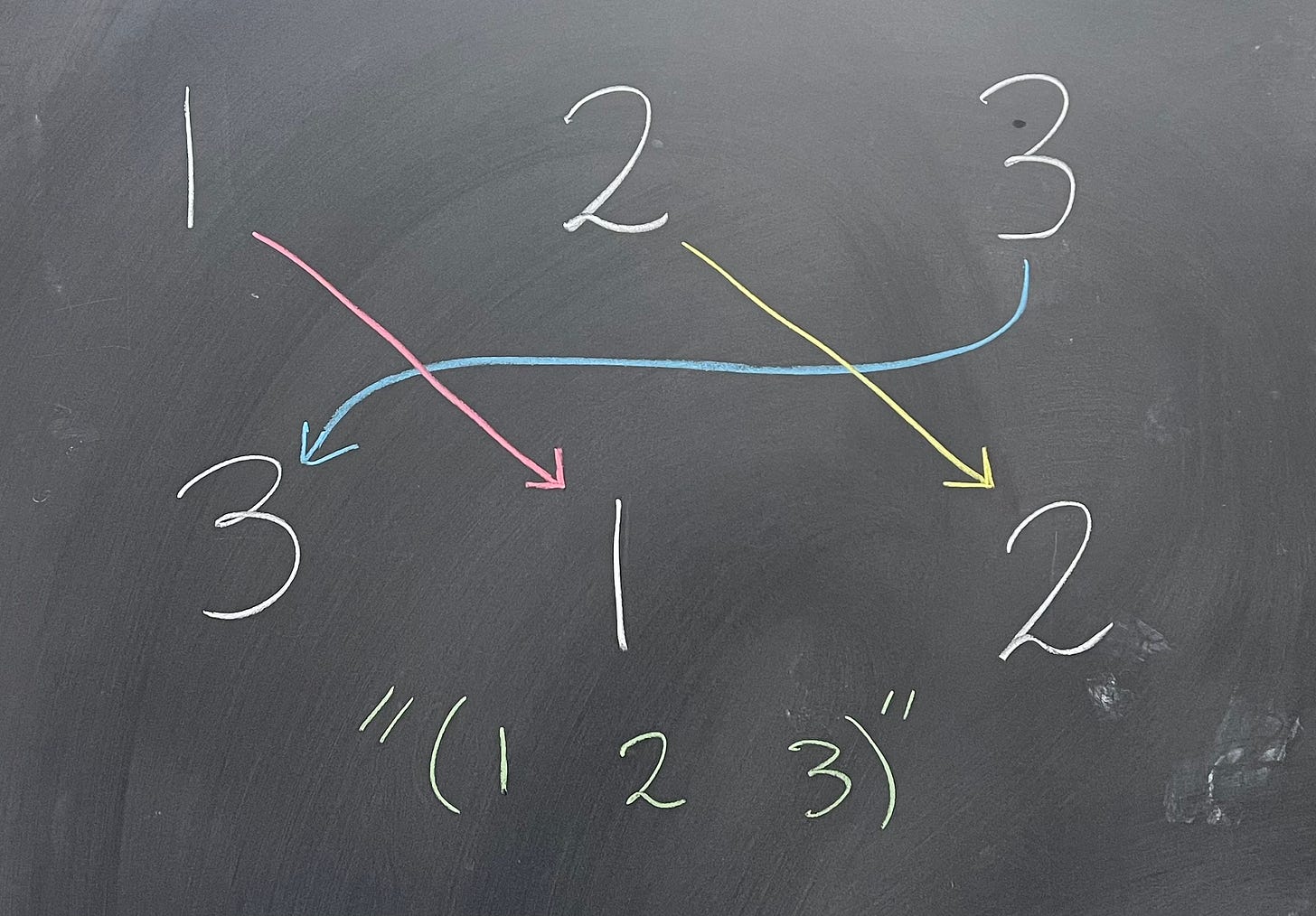
Exercise #2... 😁
🧠 🔫... anyhow. Thanks for the puzzles ☺!