Introduction to Group Theory IV
How can we know when groups are "similar"?
Last time we covered the notion of subgroups of groups. During that expedition, we came across a weird example: the group S_3 has three subgroups, which we called H, J and K. These subgroups have the underlying sets
What's weird is that all three of these groups appear to actually be the same group. If we relabeled each swap as g, then all three of these sets would look identical, and the underlying group would appear to be the same. This is what we're going to talk about today.
Homomorphisms
What we're going to do next may at first seem very strange. Why? Because I'm going to reframe this "sameness" of H, J, and K in a very formal way, which may appear unnecessarily abstruse and convoluted. We're going to define a kind of function that obeys a certain rule, and that will be our way of showing that two groups are "similar". As usual, the big fancy words and technical-ness of mathematical definitions are potentially scary, but you already understand these concepts intuitively. Don't ever forget your intuition for things - it is occasionally wrong, but right now it is going to be correct.
Definition: Let G and H be groups. A function φ : G → H is called a homomorphism if, for all a and b in G, we have
(The weird circle thing is the greek letter phi, which is standard notation for this.) Now, I realize you're probably confused by the •_G and the •_H. I put those there because I am emphasizing that on the left, the operation inside the phi is the binary operation for the group G, while on the right, the binary operation is the operation for the group H.
This is because φ is a function that takes in things in G, and spits out things in H. So, a • b is an element of G, but φ(a) and φ(b) are elements of H. So, what this definition is saying is that a function is a homomorphism if the function "respects" the group operation. We care about functions respecting the group operations, because it tells us that the operations are "the same" to some degree - certain objects within both groups behave the same way.
As usual, when we have a technical definition, the best way to understand it is to see some examples. Let's construct a homomorphism from H to J. We let φ: H → J, and define
I have once again put H and J-labels here, but this time on the identity elements. This is to stress essentially the same fact - on the left, the identity element we are putting into phi is the identity element in H, while on the right we have the identity element in J. Since (1 2) is not in J and (1 3) is not in H, there is no need to do the same thing for them.
Let's check to make sure this is a homomorphism. We're going to check that any choice of a and b satisfies our homomorphism property. Because our groups are so small, there's only three cases to check:
a = b = e;
a = (1 2), b = e;
a = b = (1 2).
We'll just go in order. We have
If this looks like a lot of equals signs to you, that's because it is! I wanted to be very explicit, though, with every step that I'm doing here. First, we leverage the fact that "multiplying" (mathematicians are lazy and reuse words) anything by the identity will give you the original thing back. Next, we apply our definition of φ(e_H). Then we multiply the identity by the identity (which we can do since it doesn't change anything), and finally rewrote those as φ(e_H).
We'll go a little faster this time. We have
As before, we use the fact that we have the identity, and then apply our definition of φ.
Finally, we have
This means φ is indeed a homomorphism!
It's pretty clear that H, J, and K are all really the same group in terms of internal behavior. We have an identity element, and a non-identity element a, such that
Essentially, this means that H, J, and K are the same group up to the labels we use for the elements. We can see that from our homomorphism, too, because secretly our homomorphism is an isomorphism. To define what an isomorphism is, we need our language from part 2 of surjectivity and injectivity, which is part of why those concepts are so important.
Definition: Let G and H be groups. An isomorphism between G and H is a homomorphism φ : G → H that is also a bijection.
The bijection part of the definition is really important. It means that our groups have the same number of elements1. So, if they have the same number of elements, and we can find a homomorphism between them (and remember that homomorphisms "respect" the group operations), then we know that the only difference between the groups is the labels. As usual, I've just thrown a lot of theory at you, so let's do a couple examples, the second of which should be familiar (at least, if you've been doing the exercises).
ℤ_12 and its subgroups
Last time, we saw that ℤ_12 has a subgroup of size 6 - namely, the subgroup containing 0, 2, 4, 6, 8, and 10, which we called H. (Yes, this is a different H than the one we had just before.) Let's think about another group for a moment - ℤ_6. We can think of ℤ_6 as being like a much smaller clock, with only six "hours":
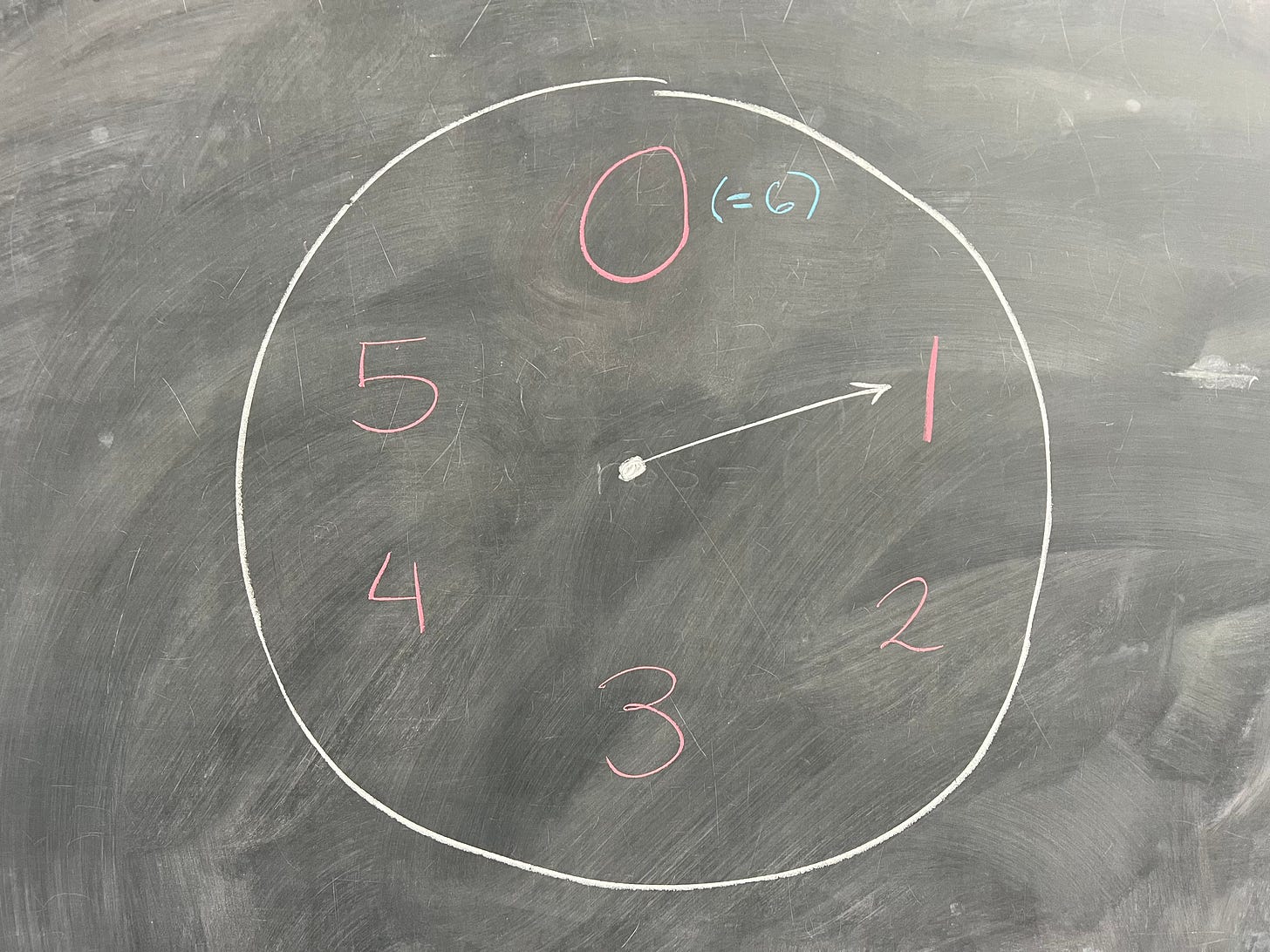
So, in ℤ_6, once we go past five and reach six, we swing back to zero. This is similar to ℤ_12 - the only difference is what our number is that we choose to be like zero. We can see some similarities between ℤ_6 and our subgroup H. In fact, we might have a suspicion these are the same group! Each element of H is exactly two times a corresponding element of ℤ_6. In fact, let's define a homomorphism φ : ℤ_6 → H by
This sends 0 to 0, 1 to 2, 2 to 4, etc. We need to check and make sure that this is a homomorphism. In this case, it's really easy to do. Let a and b both be in ℤ_6. We have
And...we're done! This shows that φ is a homomorphism. Further, since ℤ_6 and H both have six elements, and each element of ℤ_6 goes to a different element of H, we know that φ is a bijection, and therefore an isomorphism. Since we have an isomorphism between ℤ_6 and H, we say that ℤ_6 and H are isomorphic. We write this mathematically as
As we noted, because there is an isomorphism between ℤ_6 and H, we see that ℤ_6 is exactly the same as H - the only difference between them is that in one case, we are using 0, 1, 2, 3, 4, 5, while in the other, we are using 0, 2, 4, 6, 8, 10. Everything else about them is the same - the number of elements, the way elements act under their respective operations - everything.
Another interesting thing here, is that the same φ works as a homomorphism between ℤ_6 and ℤ_12. We define φ : ℤ_6 → ℤ_12 in exactly the same way:
The difference here is that, for example, there is no element of ℤ_6 that gets mapped to 1 in ℤ_12. In fact, the elements that we map ℤ_6 to are precisely and only those of H. We have a name for this - we say that H is the image of ℤ_6 under φ. In this case, φ is an injection, but not a surjection. What φ is telling us, then, is that ℤ_6 and ℤ_12 are similar - in this case ℤ_12 contains a "copy" of ℤ_6 within it.
S_3 and D_6
You might recall there being an exercise two weeks ago about finding a "correspondence" between S_3 and D_6.
Think about the groups S_3 and D_6. Do you see any relation between them? Each group has 6 elements - see if you can find some kind of natural "correspondence" between the two.
I held off on answer this exercise last week because secretly, that exercise was a hint of what we’re doing today. Let's flesh this exercise out now. For a refresher, recall that D_6 is the group of symmetries of a triangle:
The first thing that jumps out is that elements of S_3 permute three things (we think of them permuting any old numbers or objects), and the elements of D_6 also permute three things - the vertices of the triangle. Let's see if there's a homomorphism between elements of S_3 and elements of D_6.
Consider the element (2 3) - that is, the element of S_3 that swaps positions 2 and 3. Is there an element of D_6 that does a similar thing? Checking quickly, we see that what we called s appears to be the same as (2 3):
Likewise, the other reflections of D_6 correspond to (1 2) and (1 3):
Great, so all the swaps in S_3 correspond to reflections in D_6. What about the cycles? If your intuition is especially good, you might spot that cycles are the same as our rotations:
And of course, our identity elements correspond with each other, too:
Putting all of this together, what we have is:
This defines our homomorphism φ : S_3 → D_6 -- we take in each element of S_3, and have φ send it to its corresponding element of D_6. In this case, it's somewhat tedious to check that the homomorphism property is satisfied, but we'll do an example.2 Let's consider the element (1 2 3) • (2 3) in S_3, and see what φ gives us:
As we can see, our homomorphism property is satisfied, and all similar such calculations also satisfy the homomorphism property. Since φ is a bijection (left to the reader to prove/understand why), this means that φ is an isomorphism! So, we have that
You might wonder - does this hold true in general? That is, do we have, for all integers n,
Unfortunately, this is not the case in general. The easiest way to see this is to see that D_8 has 8 elements, and S_4 has 24 elements. For there to be an isomorphism, we need a bijection, and you can't have a bijection between things with different numbers of elements.
Summary
Today we covered one of the most important concepts for the overall project we're working towards: *homomorphisms* and *isomorphisms*.
Let G and H be groups. A homomorphism is a function φ : G → H such that, for all a, b in G, we have
\(\phi(a \cdot b) = \phi(a) \cdot \phi(b).\)If φ is a bijection and a homomorphism, we say that φ is an isomorphism.
If there is a homomorphism between G and H, we know that they are "similar" in some sense. If there is an isomorphism between G and H, then G and H are the same group up to the labels. In this case we write
\(G \cong H.\)
This idea seems simple, but it is incredibly powerful and will do a lot of heavy lifting for us later in the series.
Exercises
We know that S_3 and D_6 are isomorphic, but the isomorphism we found is from S_3 to D_6. Can you find an isomorphism that's from D_6 to S_3? (Keep in mind that we know an "inverse" function has to exist, since the isomorphism we found is a bijection.)
Find a homomorphism from D_8 into S_4.
Find a homomorphism from S_3 into S_4.
Solutions to Previous Exercises
We saw that there is a subgroup of size 6 for the group ℤ_12. What other sizes of subgroup exist? (Don't forget the trivial subgroup and the improper subgroup.)
When we first tried to construct a subgroup of ℤ_12, we started with H = {0, 1}. The issue we ran into was that 1 generated all of ℤ_12. What other numbers generate ℤ_12? Do you see anything interesting about those numbers in relation to the number 12?
We can solve both of these problems at once. We do this by doing the same kind of "pick an element, make sure our set is closed" action on all of our non-zero elements:
1: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
2: {0, 2, 4, 6, 8, 10}
3: {0, 3, 6, 9}
4: {0, 4, 8}
5: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
6: {0, 6}
7: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
8: {0, 4, 8}
9: {0, 3, 6, 9}
10: {0, 2, 4, 6, 8, 10}
11: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
From this, we see that the subgroups of ℤ_12 have sizes 1, 2, 3, 4, 6, and 12. We also see that the numbers which generate ℤ_12 are 1, 5, 7, and 11.
One difference when considering infinite groups is that two groups can have a bijection between them without having all the same elements. If you want to think about this, try finding a bijection between ℕ, the set of positive integers (1, 2, 3, …) and ℤ, the set of integers (…, -2, -1, 0, 1, 2, …).
Generally, when we define a homomorphism, it will not be defined in this “piece-wise” manner, because it makes it difficult to prove that the homomorphism obeys the rule. Instead, our homomorphisms will generally look like φ(x) = 2x, or φ(y) = y^4, something like this. It’s much easier to verify that we do indeed have a homomorphism that way.


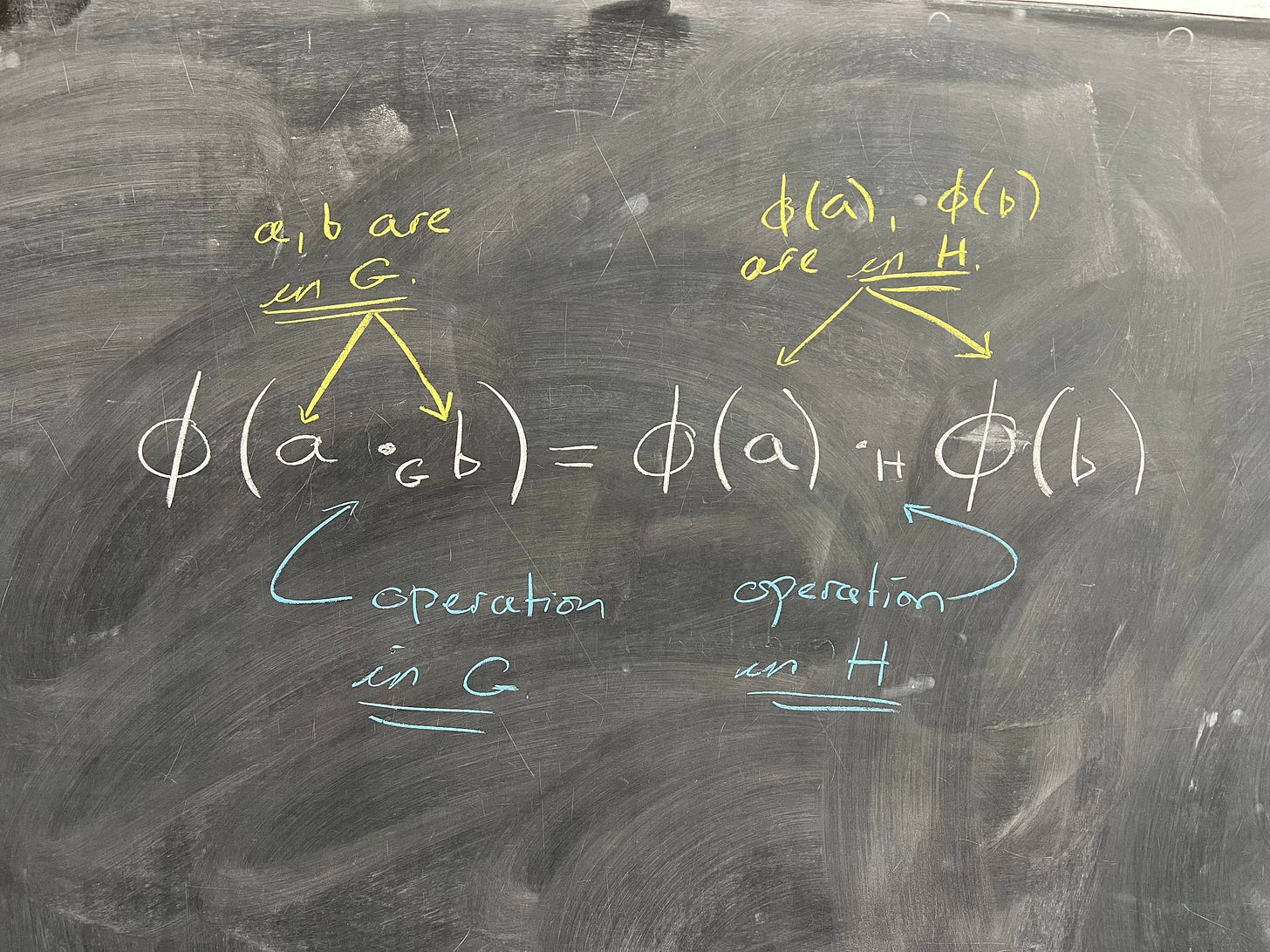
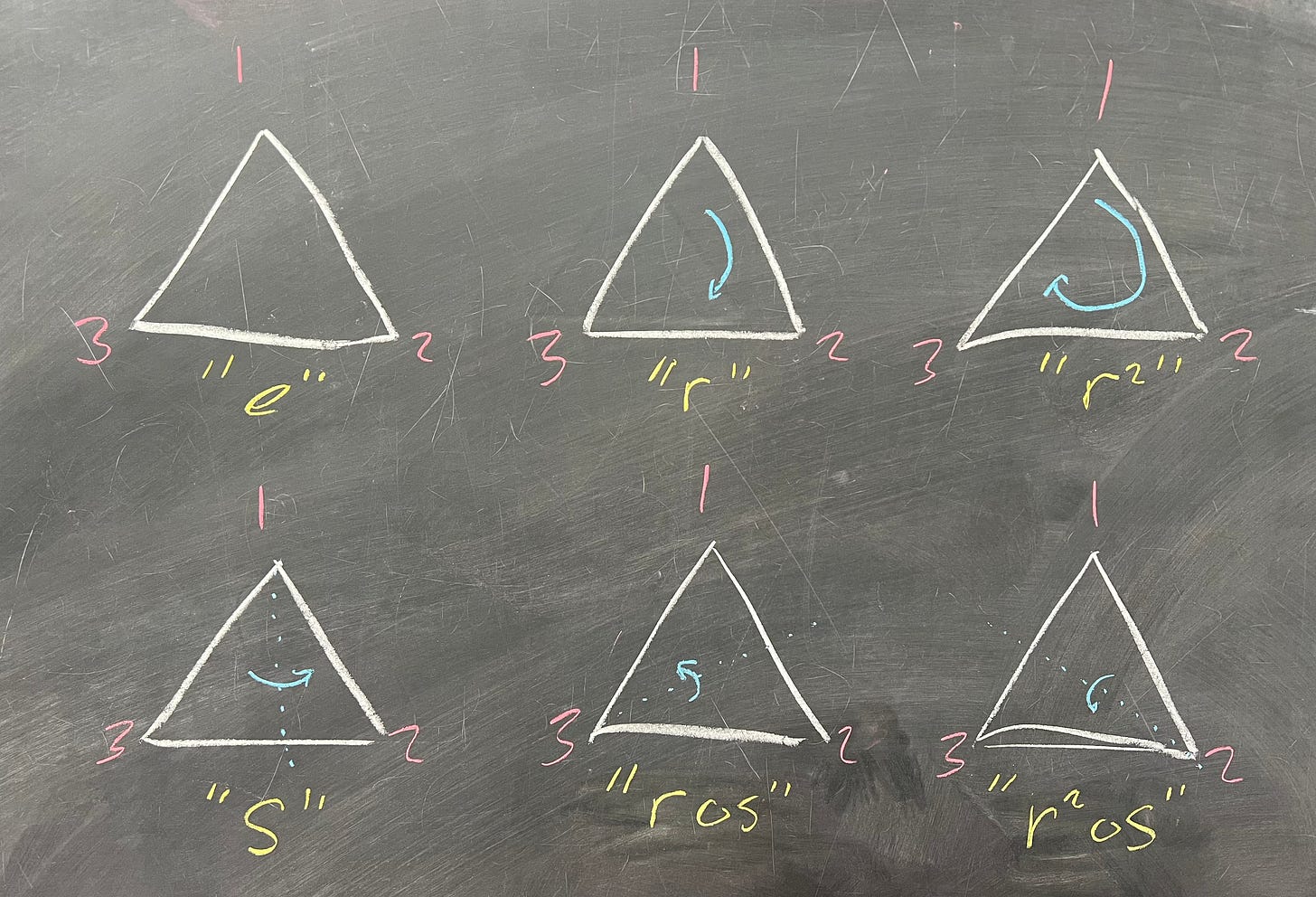
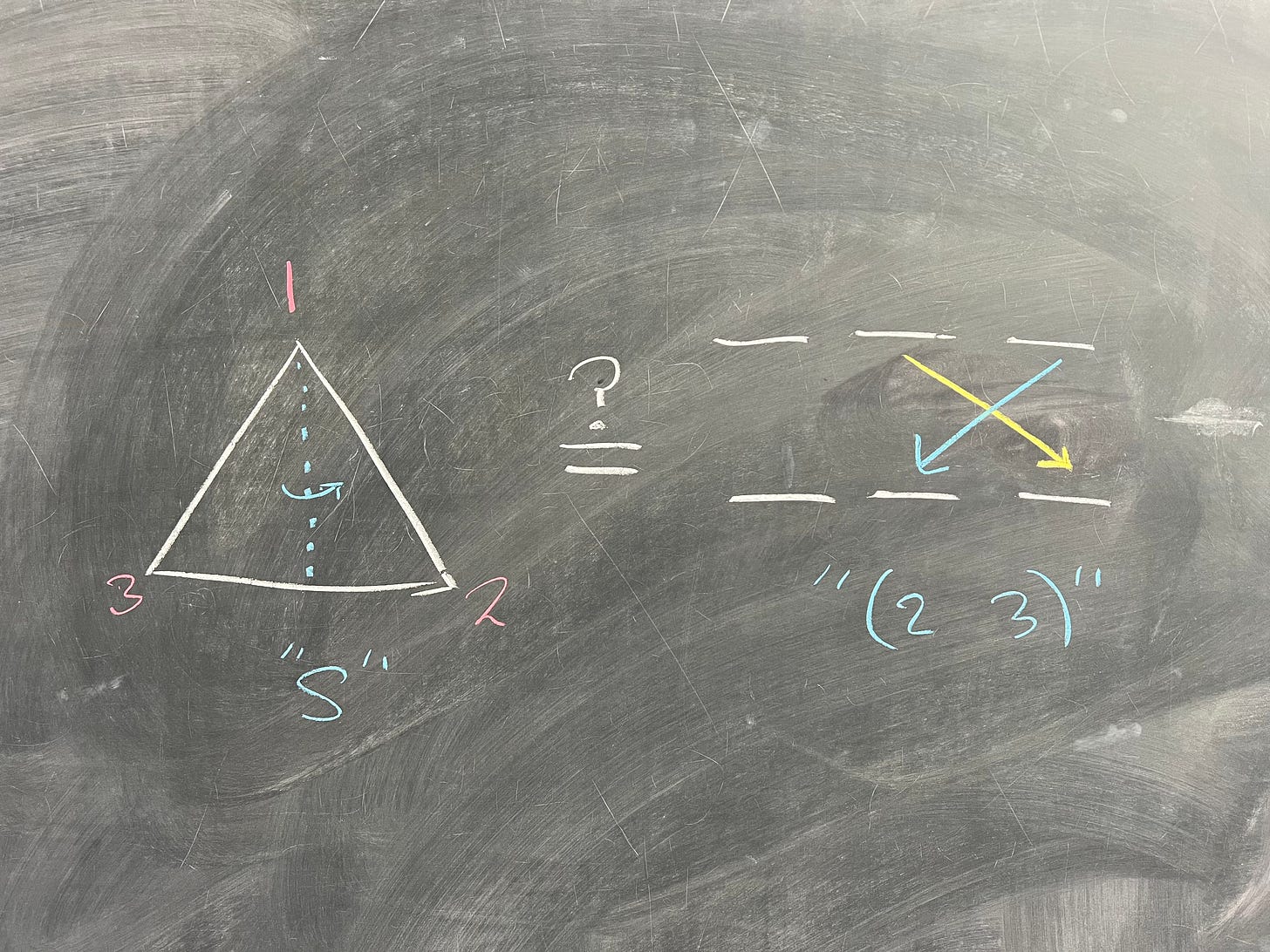
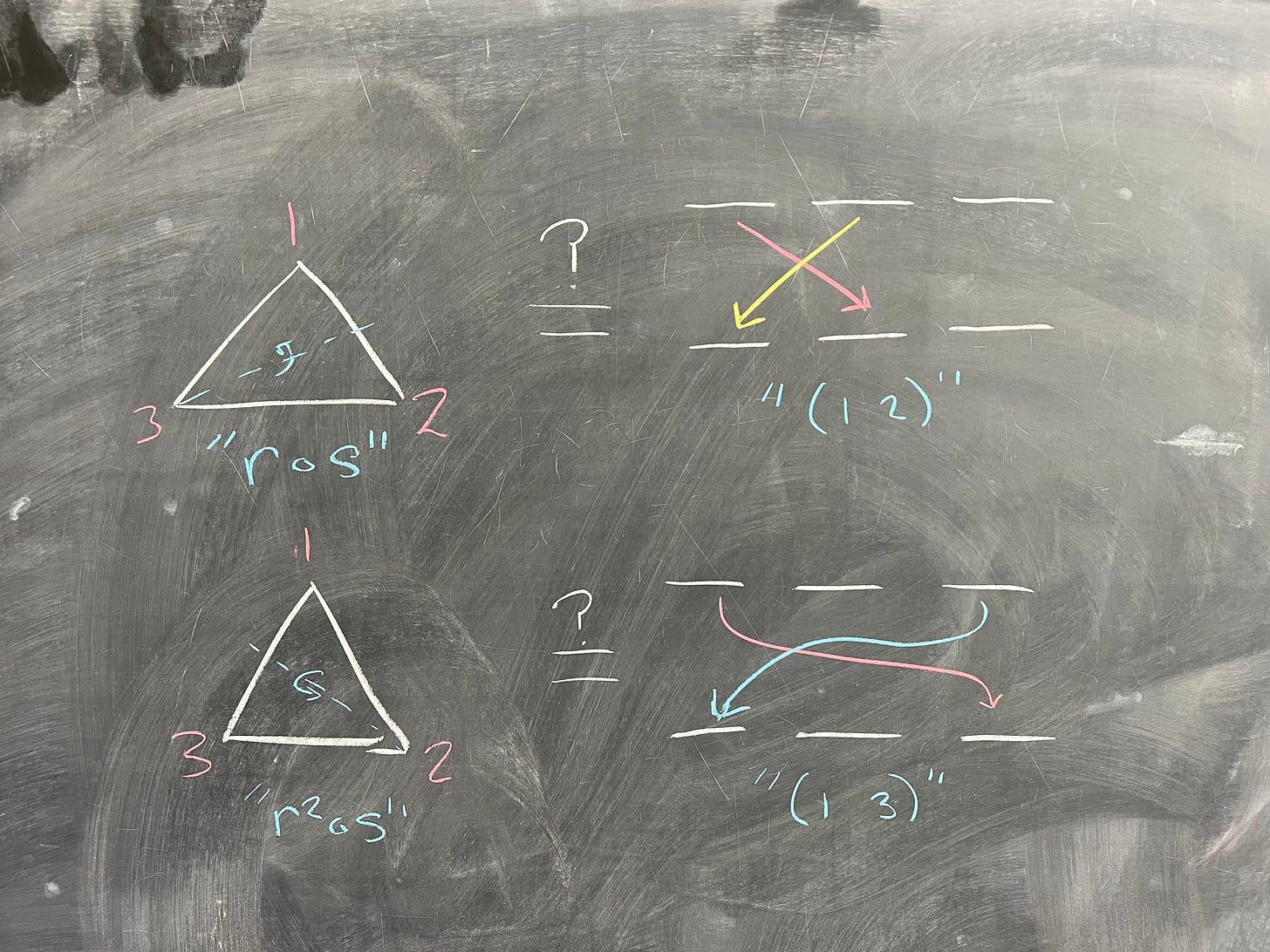
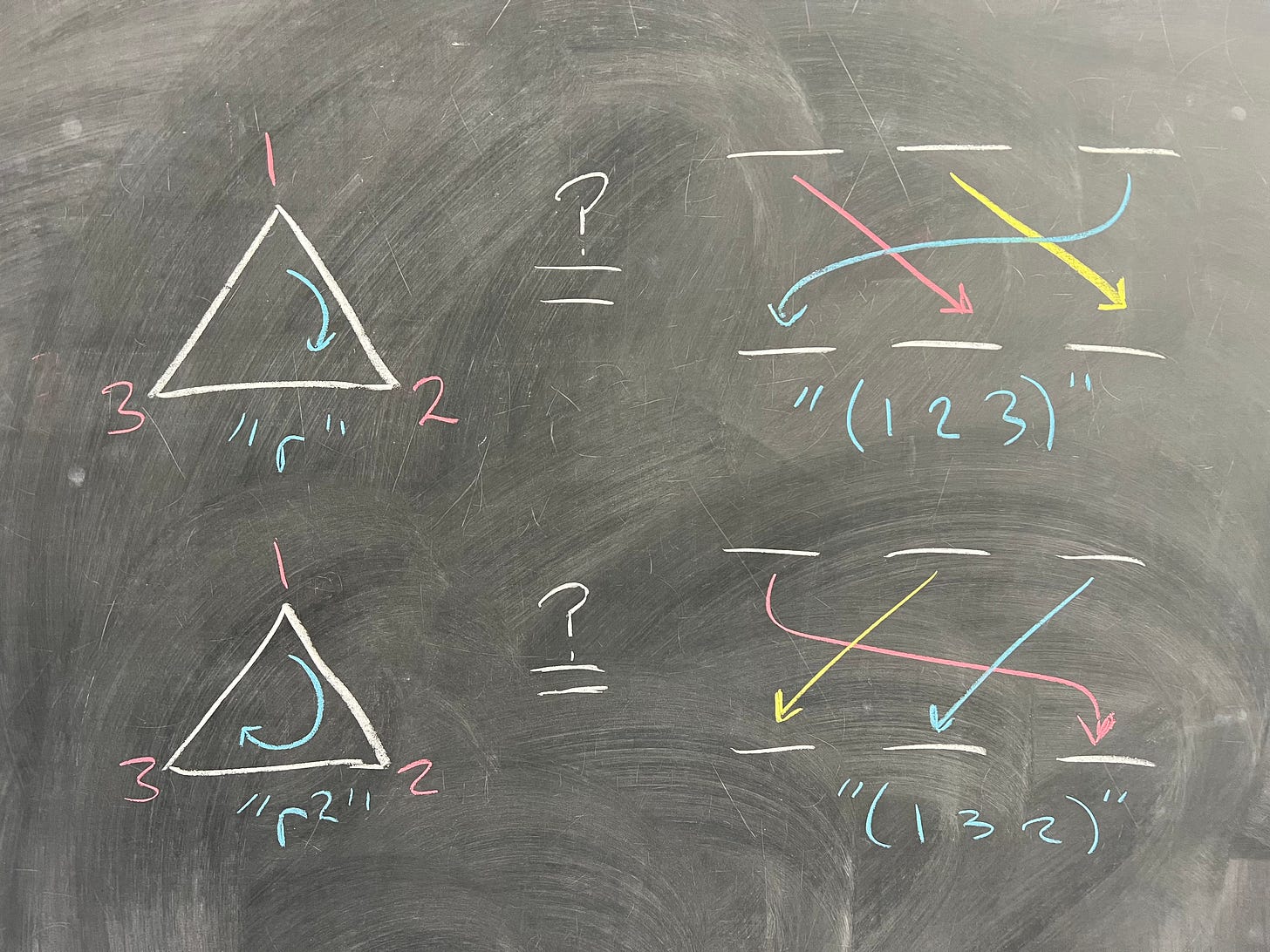
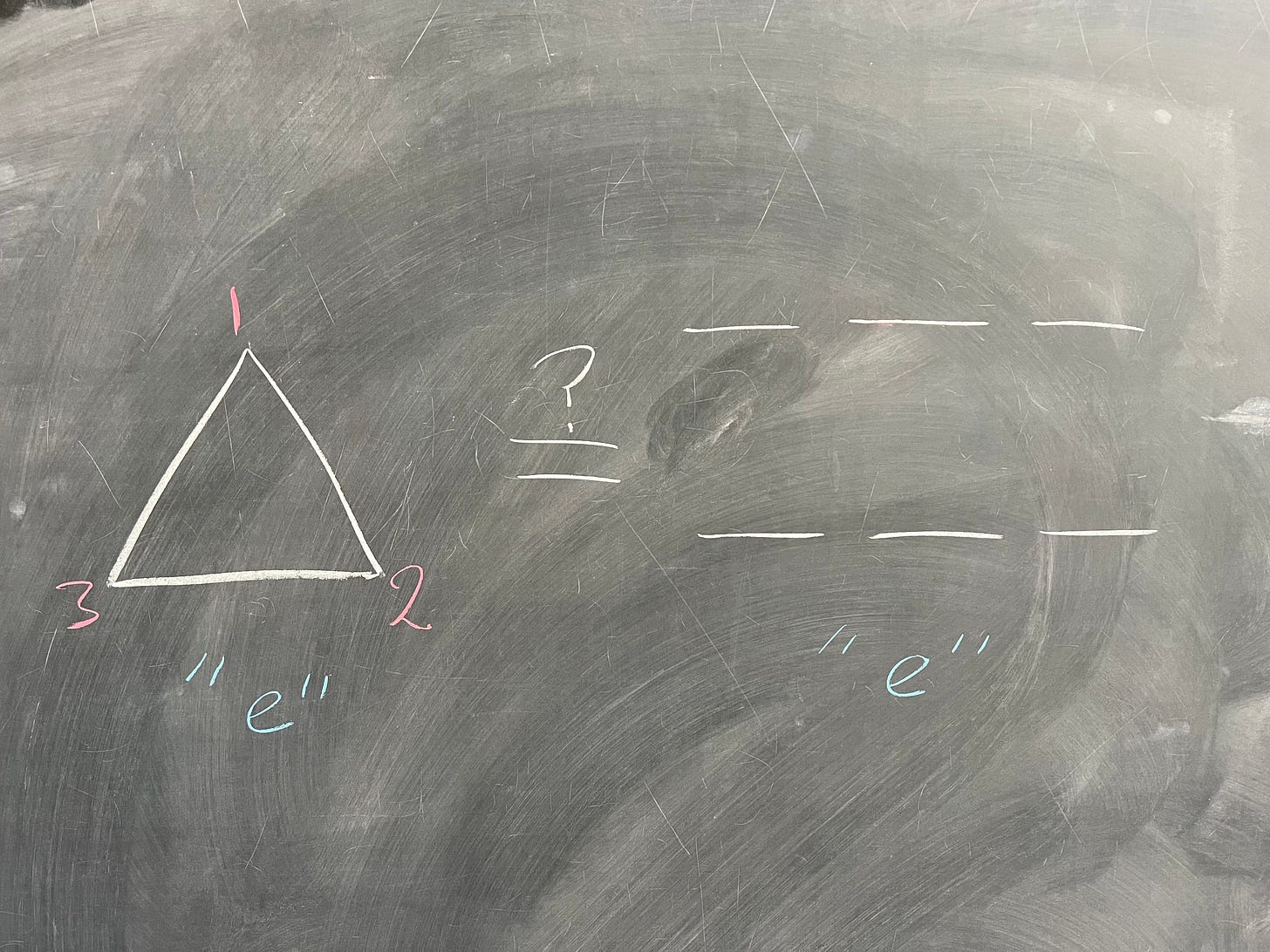
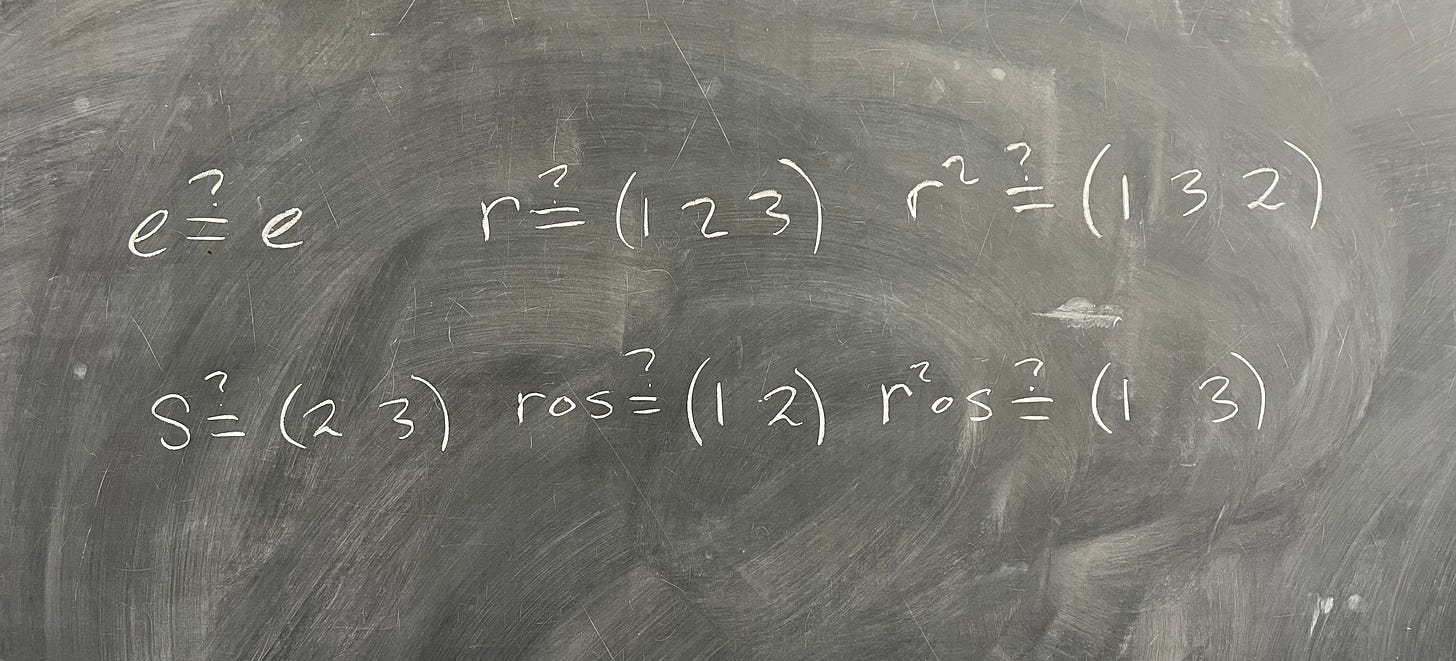
Good series! Getting into some new territory for me with homomorphisms and isomorphisms (although I was familiar with the general notion of isomorphic).
What was fun about the subgroups of Z_12 was the connection to the factors of twelve: 2, 3, 4, and 6. I banged out a simple Python app to generate the subgroups for any Z. The subgroups with sizes smaller than Z are always from factors of Z. I hadn't ever realized that connection. Cool!