Introduction to Group Theory VI
Apologies for the wait on this article − I've been preparing for a complex analysis qualifying exam that I have to take later this week. At the behest of my mother (thanks mom!) I've also put together a list of definitions that we've used so far, which I will update periodically. It can be found here.
Mathematicians have two (2) modes of thought when it comes to naming things mathematically:
Come up with some arcane bullshit that no human has ever uttered before and then make everyone use it − "epimorphism" or "arborescence", anyone?
Take some poor, innocuous, everyday word and give it mathematical meaning (with bonus points for giving it more than one meaning). "Group", "Ring", and "Normal" are just a few examples.
In fact, for the next few weeks we will be talking about the last example given of the latter kind − specifically, Normal subgroups. Normal may well win the award for the most different mathematical use cases, as this wikipedia list shows:
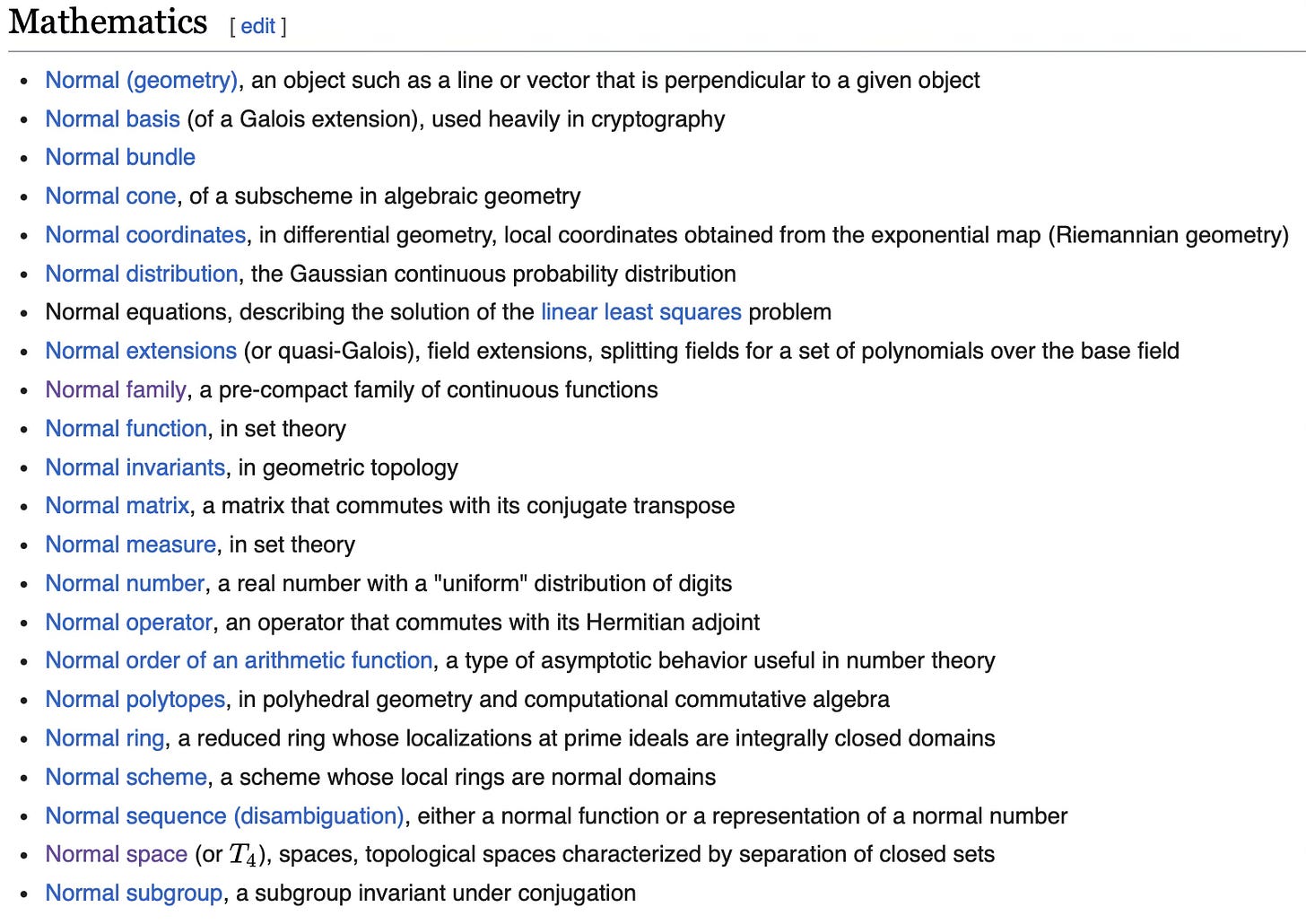
Along the way to defining normal, we'll define what a coset of a set is, and we'll use that to prove a famous theorem that you may have already picked up on. So far, whenever we've had a group G with a subgroup H, the order of H has always divided the order of G. Using cosets, we'll be able to show that this is always the case − a result known as Lagrange's Theorem.
Cosets
Let G be a group, and H be a subgroup of G. We're going to define a "relation" between elements of G. Don't think too hard about this word "relation" − it's exactly what it sounds like. We're just going to set some condition and say that "a and b are related if they satisfy condition (x)". Let a and b be related if and only if a⁻¹b ∈ H.1 If a and b are related, we will denote this by
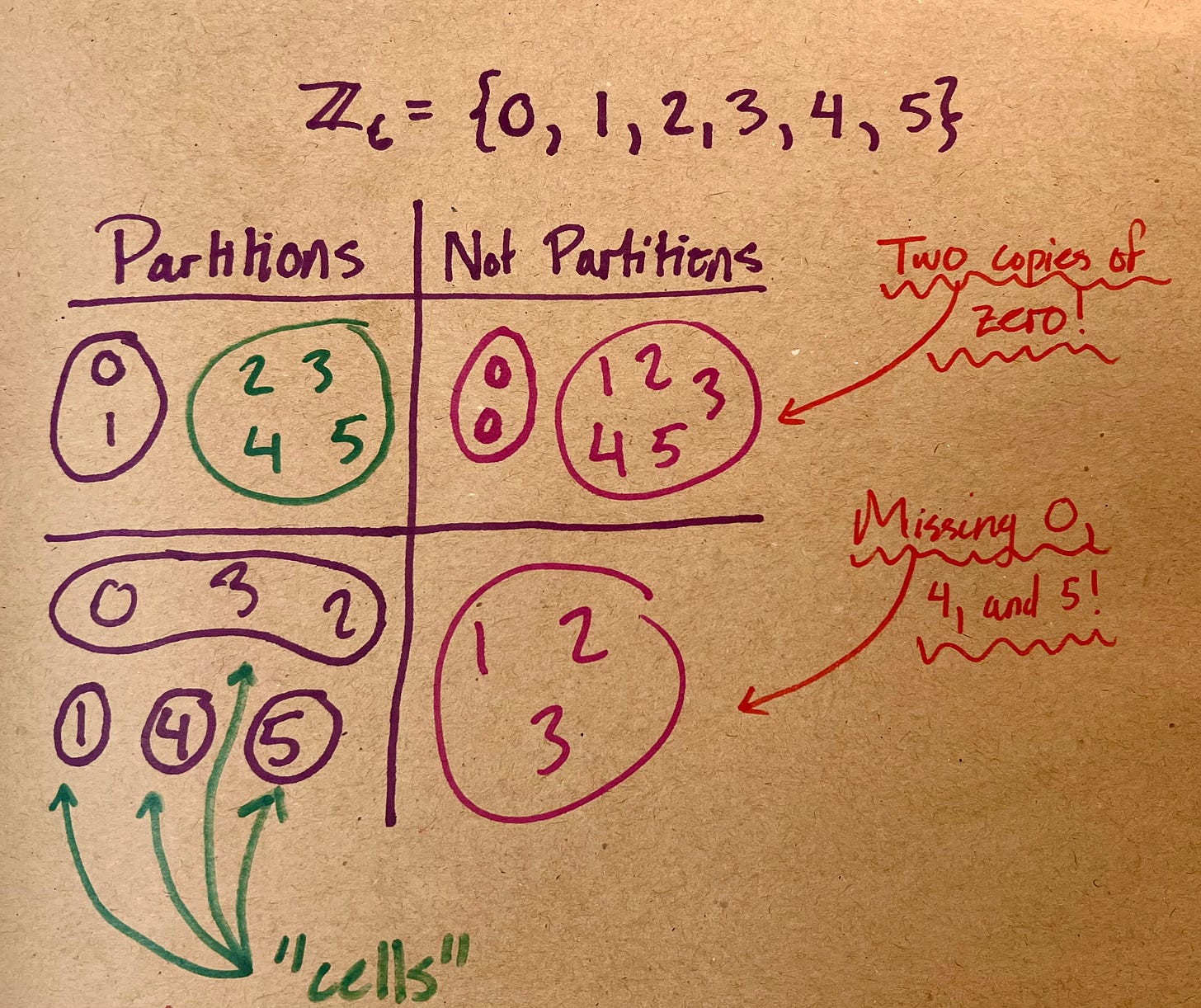
Now, because of time constraints (and because it really isn't all that interesting) I will be doing some hand−waving. It can be shown that ∼ is an equivalence relation. If you've never heard this term before, don't worry about it. The important thing about equivalence relations is that they automatically partition your set. What this means is that if I take all the elements that are related to each other and sort them into piles, then each element will occur in exactly one pile. Don't worry − we'll do an example or two so you can see what all this means.
Here we see a couple partitions of the group ℤ₆, and a couple examples of things that do not partition ℤ₆. The partitions both have every number in ℤ₆ precisely once; the non-partitions either have more than one copy, or are missing some numbers. Additionally, the partitions of ℤ₆ divide everything into piles that do not overlap - in the first partition, if 2 were in both the green and the purple pile, then it would not be a partition.
Mathematicians (of course) have a term for the different piles − they are called the cells of a partition.2 Let's see what these cells look like. Choose some a ∈ G. The cell containing a consists of all the x ∈ G such that a ∼ x. By definition, this means all the x such that a⁻¹x ∈ H. Now, a⁻¹x ∈ H exactly when a⁻¹x = h for some h ∈ H. Multiplying by a gives
So, the cell containing a is all the elements that have the form ah for some h ∈ H. We denote this set aH.
Definition: Let G be a group and H be a subgroup of G. The subset
is called the left coset of H containing a.3 (Note that the "operation" being expressed in aH is that of the group. So, when we see an example where the group operation is addition, our coset will be written a + H.)
The cells of our partition are exactly the same as the left cosets of H. For our first example, we'll use a group everyone should be very familiar with now: D₆. Consider the subgroup H = {e, r, r²}. Since there are only 6 elements in D₆, we'll just show the cosets for every element:
If you aren't sure, double−check the calculations yourself to see that indeed, r²sH = sH. I said this in the first article, and I'll say it again − there is no substitute for doing the math. And – and! – if you've made it this far, you are clearly capable of doing the math involved here.
From this, we see that there are two cosets of H in D₆ − namely, H and sH. We could, of course, choose to label this as H and rsH, or rH and r²sH, but there's no reason to do that when this is so much simpler. Also, note that H and sH form the cells of a partition, as we discussed. Each element of D₆ is either in H or sH, but not both.
Let's do one more example. Consider H = {0, 3, 6, 9} as a subgroup of ℤ₁₂. Then there are three (unique) cosets of H in ℤ₁₂:
Once again, we know that the cosets of H form a partition of ℤ₁₂, and indeed we see that each number in ℤ₁₂ is represented exactly once. Also, it’s worth pointing out that if we try something like 5 + H, we get
because 9 + 5 = 14, and we subtract 12 to get 2. Remember that we have to subtract 12 if we go over, because we’re working in ℤ₁₂ here. 5 + H is a perfectly valid thing to think about - it just is the same as 2 + H here.
In both of our examples, there's been a pattern: each coset of H has the same size as H. This seems intuitively obvious, but there are lots of mathematical statements that seem "intuitively obvious" but are false, so let's actually prove that the cosets of any subgroup H have the same size as H.
Theorem: Let H be a subgroup of G. Then for any a ∈ G, the coset aH has the same size as H.
Proof: Any time we want to show a claim of the form "X and Y have the same size", we should try to construct a bijection. Let f : H → aH be defined by f(h) = ah. To show that f is an injection, we need to assume that f(b) = f(c) and then show that b = c. Well, if f(b) = f(c), then we have
So, f is an injection. Now suppose y ∈ aH. Then there exists some h ∈ H such that y = ah, by definition of aH. But then, y = ah = f(h), so f is a surjection. Since f is a surjection and an injection, it is a bijection, which means H and aH have the same size. ☐
This leads us to:
Theorem: (Lagrange's Theorem) Let H be a subgroup of a finite group G. Then the order of H is a divisor of the order of G.
Proof: Let G have order n and H have order m. Further, let r be the number of cells that the cosets of H partition G into. Then, since the cosets form a partition, they must contain each element of G exactly once, which means n = rm. Thus, m divides n. ☐
Cyclic Groups
One very nice result you can get from Lagrange's Theorem has to do with cyclic groups. You might recall that I vaguely gestured my hands in the direction of cyclic groups all the way back in part 3. It is here that I will define them more explicitly.
Definition: Let G be a group and a ∈ G. Then the set {aⁿ | n ∈ ℤ} is called the cyclic subgroup of G generated by a. We denote this group by ⟨a⟩ and say that a is a generator of ⟨a⟩.
Now, it's not immediately clear that this set even forms a group, so let’s prove that it does. We need to show three things for this to be a group:
The binary operation inherited from G must be closed on ⟨a⟩.
⟨a⟩ must contain the identity element.
For each x ∈ ⟨a⟩, we must also have x⁻¹ ∈ ⟨a⟩.
We do not need to check associativity, since the operation is associative on all of G (which contains ⟨a⟩.) For closure, we have aʳaˢ = aʳ⁺ˢ ∈ ⟨a⟩. The identity is in ⟨a⟩, since a⁰ = e. And, for any aʳ, the inverse is a⁻ʳ ∈ ⟨a⟩. So indeed, ⟨a⟩ is a subgroup of G.
Of course, we can consider groups that exhibit this cyclic property without being a subgroup of some bigger group. ℤ₁₂, for example, is a group we've seen that is a cyclic group. It is generated by 1, but it is also generated by 5, 7, and 11. (Check this, if you like.) Of course, there's nothing special about 12 here: for any positive integer n, the group ℤₙ is a cyclic group of order n. Importantly for our next theorem, this includes the cases where n = p, for some prime number p.
Theorem: Every group of prime order is cyclic.
Proof: Well, before we get to the proof, stop and think for a moment about this claim. Really? Every group of prime order is cyclic? There is not a single group that has a prime number of elements that is not cyclic? There are an infinite number of primes: 2, 3, 5, 7, 11, 13, ... — how would we possibly prove such a claim? It seems outlandish! And yet, Lagrange's theorem gives this to us, almost for free.
Let G be a group of order p, where p is some prime, and consider a ∈ G such that a is not the identity. Then the group ⟨a⟩ must contain at least 2 elements: e and a. But by Lagrange's theorem, the order of ⟨a⟩ must divide the order of G, and |G| = p is a prime, which only has two divisors — 1 and p. Since |⟨a⟩| is bigger than 1, it must have order p − meaning ⟨a⟩ = G. Thus, G is cyclic. ☐
This is an incredibly beautiful result! Think about the elegance here — we're using Lagrange's theorem, which is essentially a result about counting, and from this we have shown that there is only one kind of group with prime order, namely, cyclic groups.
The number of cosets of H in G seems like an important thing to keep track of, which leads us to the following definition:
Definition: Let H be a subgroup of G. The number of cosets of H in G is called the index of H in G, which we denote (G : H).
What about right cosets?
Everything we've done so far has been using left cosets − that is, the cosets of the form aH = {ah | h ∈ H}. We could've easily done things, however, with the right cosets of H, which have the form Ha = {ha | h ∈ H}. All the results we proved, e.g., Lagrange's Theorem, can be done with only minor modifications to use right cosets instead of left cosets. The reason we have to differentiate them, though, is that often times the right cosets and the left cosets are not the same. As usual, we'll do an example to see this.
Let H = {e, s} be a subgroup of D₆. It has three left cosets and three right cosets. The left cosets are:
eH = {e, s} = H;
rH = {r, rs};
r²H = {r², r²s};
while the right cosets are:
He = {e, s} = H;
Hr = {r, sr};
Hr² = {r², sr²}.
Since rs = sr² ≠ sr, we have rH ≠ Hr. So, the right cosets and the left cosets are not the same. If they were always the same, we could just drop the "left" and "right" parts. (In fact, anytime they do happen to line up, we will just drop the left and right and refer to "cosets". Mathematicians are lazy.) It might seem like this is an unimportant difference, but very curious things happen when the left and right cosets are the same. Let's do an example. Consider H = {0, 3} as a subgroup of ℤ₆. Since ℤ₆ is an abelian group, the left and right cosets are guaranteed to be the same (why?), which means our three cosets (see? lazy.) are:
H = {0, 3};
1 + H = {1, 4};
2 + H = {2, 5}.
If we write down a table showing the addition of these elements, but sort them by coset, something weird happens:
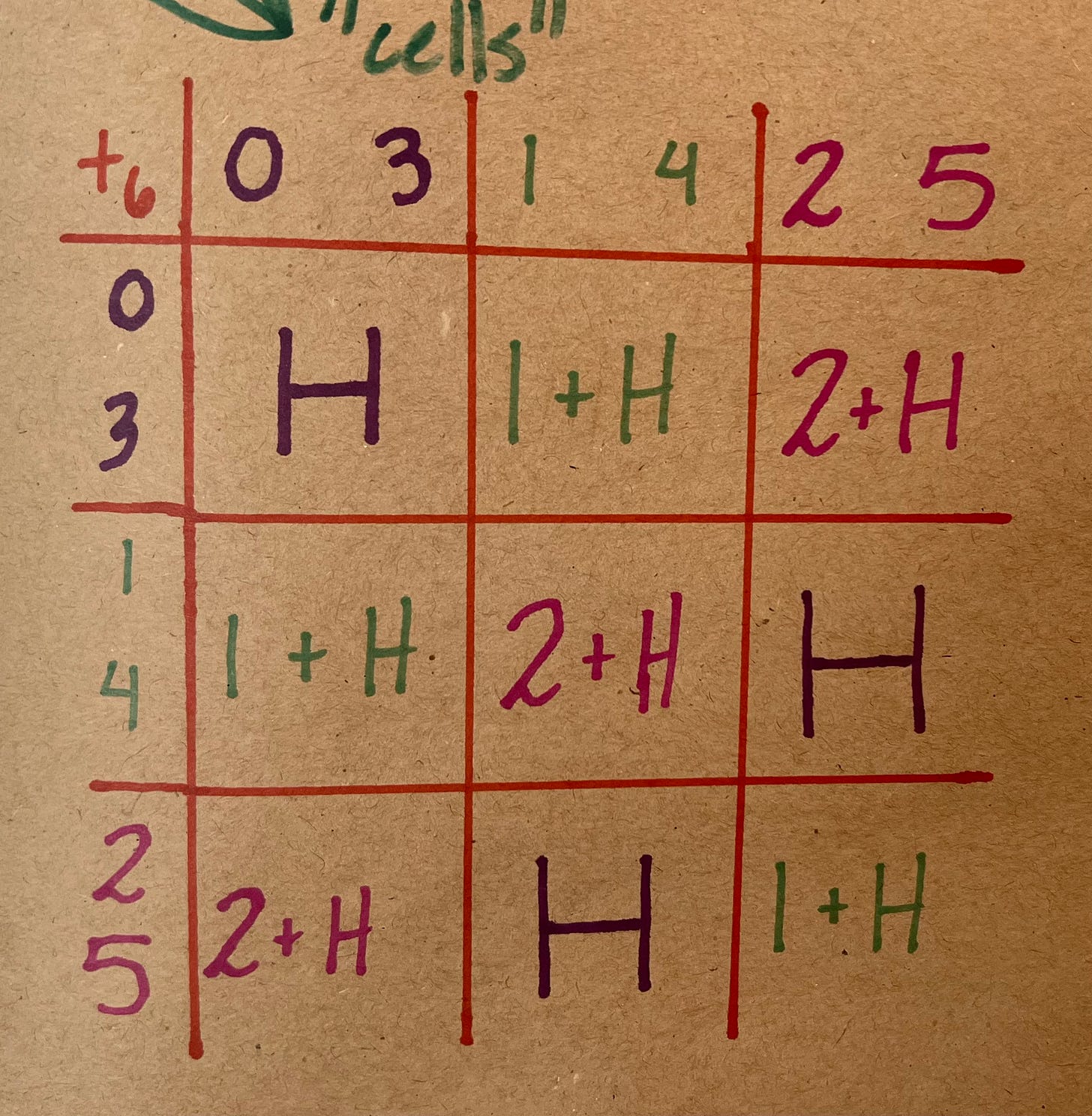
We get nine different squares within the table. This becomes more explicit if, instead of doing the addition, I just note down which coset the added elements are in:
If I just drop the H entirely, this table looks suspiciously like another table, that of ℤ₃:
What this tells us, then, is that the cosets of H form a group, and it is isomorphic to ℤ₃. Strange, very strange...
It is here that we will define the word normal for our context. Next time, we'll get to unpack what normal subgroups really are and, more importantly, why they are so important.
Definition: Let H be a subgroup of G. We say that H is a normal subgroup of G if for all g ∈ G, gH = Hg. We denote this by H ⊴ G.
Summary
Today we laid the groundwork to define what a normal subgroup of a group is. Doing this required that we
define the left and right cosets of a subgroup H of a group G;
prove Lagrange's theorem;
and show that the left and right cosets are not always the same.
Next time, we'll get to dig our teeth into normal subgroups and see what makes them so important.
Exercises
Compute the cosets of 5ℤ = {..., −10, −5, 0, 5, 10, ...} in ℤ. Make sure you understand why the left and right cosets have to be the same!
Find a subgroup of D₈ that does not have the same left cosets as right cosets; that is, find a subgroup of D₈ that is not normal.
Let G be a group with order 48. What are the possible orders of subgroups of G?
Solutions to Previous Exercises
In the proof of our first theorem, we left it to the reader to show that K contains the identity and inverses. Show that K indeed contains the identity and inverses.
Since K = {g ∈ G | ϕ(g) ∈ K'}, and K' is a group, we must have that e' ∈ K', which means ϕ(e) ∈ K'; hence K contains the identity. Let k ∈ K. We want to show that k⁻¹ is also in K. Since k ∈ K, we know that ϕ(k) ∈ K'. Because K' is a group, we must also have ϕ(k)⁻¹ = ϕ(k⁻¹) ∈ K$. But this, of course, means that k⁻¹ ∈ K.
Using the homomorphism you found last week from D₈ into S₄, compute the images of the sets A = {e, s} and B = {e, r, r², r³}.
I will be using the homomorphism I constructed from D₈ into S₄ − yours may well be different. We have
and
Construct a homomorphism from S₃ to S₄ with non−trivial kernel.
There's a very cheeky solution here. (For a non−cheeky solution, check out Wyrd Smythe's solutions here.) For all g ∈ S₃, define ϕ(g) = e. Then ϕ is a homomorphism, with ker(ϕ) = S₃.
I am trying to find a way to not have to manually replace LaTeX with unicode when I transfer the installments over to Substack; there is a website that does this, but for whatever reason the way it renders a^{-1} (a⁻¹) makes the minus sign nearly invisible. It’s probably safe to assume, though, that if I have a 1 in the exponent, there’s a negative there too.
Unlike some mathematical names, “cells” actually seems pretty reasonable to me. Just like our bodies are made up of cells, and each cell cannot be inside/overlap with another cell, the cells of a partition make up its parent set.
The reason we are specifying “left” cosets here is that soon, we will introduce right cosets as well.


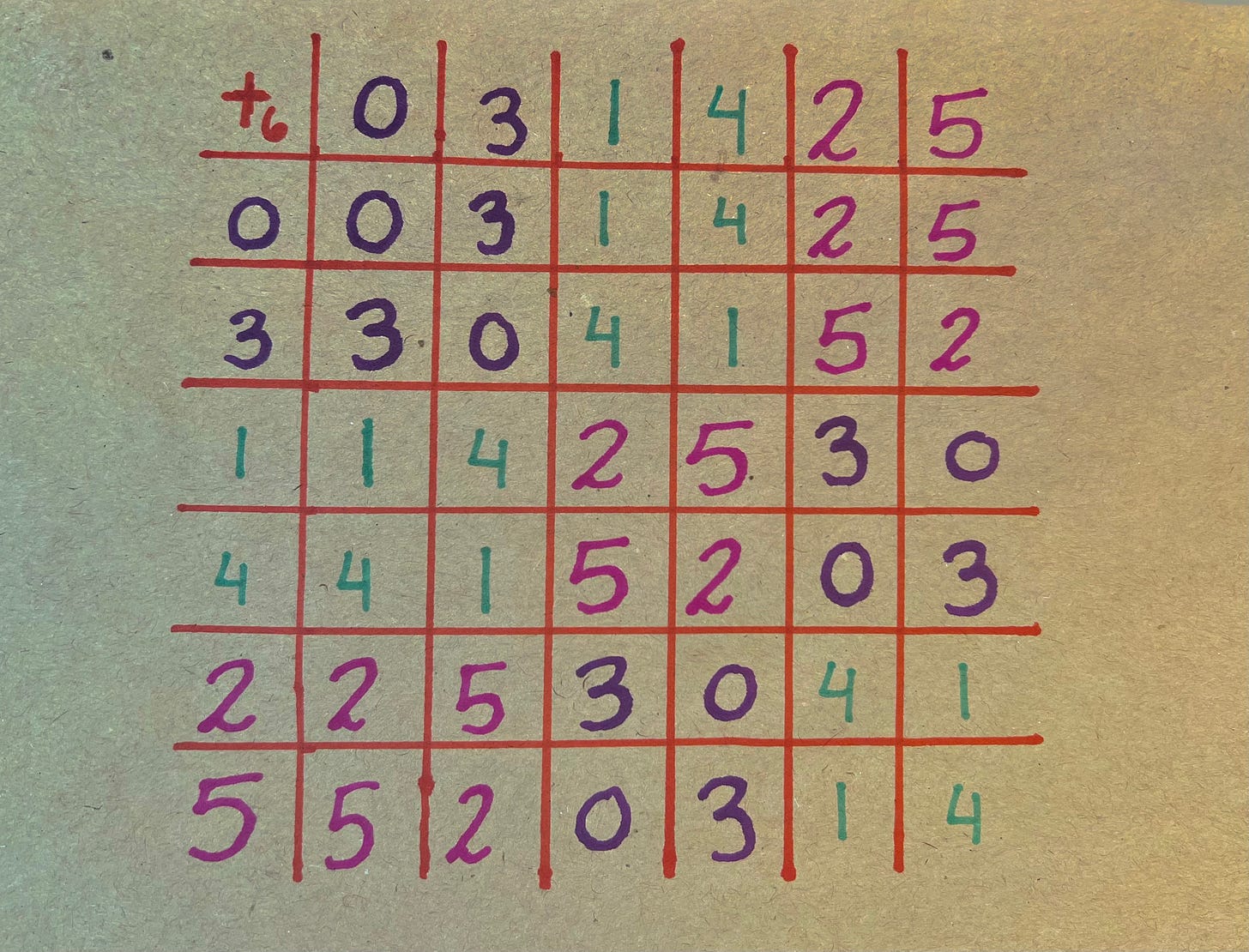
I have a question about the condition (a⁻¹x ∈ H). I tried that with the exercise 2 subgroup H={e, s}, and found that multiplying them one way always gave me s (which satisfies s ∈ H), but in some cases the multiplication didn't commute, and I got, in all four exceptions, sr² (which is not in H).
Not that my answers for exercise 2 are necessarily correct, but is this result because the subgroup isn't normal, or is it sufficient that there exists an ab ∈ H?
FWIW, I've decided to start a "homework and notes" page on my blog here. I may continue to also post answers in a restack, but I may just start adding to that page. (I find the difference between Notes text and post/page text downright weird here.)
https://logosconcarne.substack.com/p/group-theory-notes-and-homework
Ha! So, in my answer to #3 for last time, I stumbled on the three-member cosets of D₆ without knowing it.
FWIW, the problem with x⁻¹ seems to be font related. Substack uses the "Spectral" font in the post's text, and it apparently doesn't have a good implementation of the Unicode "superscript minus" character (U+207B). Post comments use a different font entirely, so it works fine here.